Name 
- ℵ-preparacompact
Definition 
- A Hausdorff space X is called preparacompact if each open cover of X has an open refinement
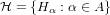 such that if
such that if
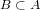 is uncountable and if
is uncountable and if
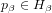 and
and
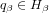 for each
for each
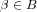 with
with
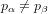 and
and
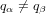 for
for
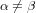 , then the set
, then the set
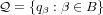 has a limit point iff the set
has a limit point iff the set
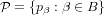 has a limit point.
has a limit point.
Reference 
- Davis, S.W. and Smith, J.C., The paracompactness of preparacompact spaces., Topology, Proc. Conf., Vol. 4, No.2, Ohio Univ. 1979, 345-360 (1980).
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ