Definition 
Suppose that if U is an open cover of a topological space X, there exests a sequence
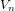 of open covers and for every point x in X, there exists an index m and W in U such that
of open covers and for every point x in X, there exists an index m and W in U such that
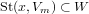 .
.
Then X is called σ-compact.
Property 
- Let X be a topological space. The following are equivalent.
- X is σ-paracompact.
- Every open cover of X has a σ-discrete closed refinement.
- Every open cover of X has a σ-locally-finite? closed refinement.
- Every open cover of X has a σ-closure-preserving? closed refinement.
Reference 
Dennis K. Burke, On subcompact spaces, Proc. Amer. Math. Soc. Vol.23 No.3 (1969) pp.655-663.
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ