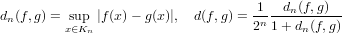hemicompact

Definition

A topological space is said to be hemicompact if there is a sequence of compact subsets (called admissible sequence) such that every compact subset is contained in some member of the sequence.

Property

• A hemicompact space is the union of the admissible sequence since every singleton in the space is a compact set.
• Every first countable hemicompact space is locally compact.
• If X is hemicompact, then the space C(X) of all continuous functions from X to the real is metrizable. The metric is given by
  
  where K_n are the admissible sequence.

Reference

Willard, Stephen, General Topology, Dover (2004).