Definition 
- A topological space X is called locally compact if every point of X has a compact neighbourhood.
Property 
- Every locally compact Hausdorff space is Tikhonov?.
- Every locally compact, paracompact Hausdorff space is strongly paracompact.
- For every compact subspace A of a locally compact space X and every open set V that contains A there exists an open set U such that
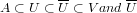 is compact.
is compact. - If X is locally compact space, then every subspace of X that can be represented in the form F∩V, where F is closed in X and V is open in X, also is locally compact.
- Every locally compact subspace M of a Hausdorff space X is an open subset of the closure of the set M in the space X, i.e., it can be represented in the form F∩V, where F is closed in X and V is open in X.
- The sum
 is locally compact if and only if all spaces X_s are locally compact.
is locally compact if and only if all spaces X_s are locally compact. - The Cartesian product
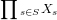 , where
, where
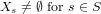 , is locally compact if and only if all spaces X_s are locally compact and there exists a finite set
, is locally compact if and only if all spaces X_s are locally compact and there exists a finite set
 such that X_s is compact for
such that X_s is compact for
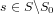 .
. - If there exists on open mapping f:X→Y of a locally compact space X onto a Hausdorff space Y, then Y is a locally compact space.
- For every locally compact space X and any quotient mapping g:Y→Z, the Cartesian product f=Id_X×g;X×Y→X×Z is a quotient mapping.
- If X is locally compact, then for every topological space Y the compact-open topology on Y^X is acceptable.
- Every locally compact paracompact space X can be represented as the union of a family of disjoint closed-and-open subspaces of X each of which has the Lindeloef property.
- Every non-empty hereditarily disconnected locally compact space is zero-dimensional.
- Hereditary disconnectedness, zero-dimensionality and strong zero-dimensionality are equivalent in the realm of non-empty locally compact paracompact spaces.
- For every non-emty locally compact paracompact space X the conditions ind X=0, Ind X=0 and dim X=0 are equivalent to hereditary disconnectedness of X.
- a coarsest uniformity? on a Tykhonov? space X exists if and only if the space X is locally compact.
- Every locally compact preregular space is completely regular.
- Every locally compact Hausdorff space is a Baire space.
- A subspace X of a locally compact Hausdorff space Y is locally compact if and only if X can be written as the set-theoretic difference of two closed subsets of Y.
Reference 
John L. Kelley, General Topology, Springer (1975).
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ