Definition 
- A topological space X is called monotonically orthocompact provided that there is an operator T: E →S from the set E of all open covers of X to the set S of all transitive neighbornets of X such that
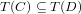 whenever
whenever
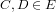 and C is a refinement of D , and such that
and C is a refinement of D , and such that
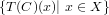 refines ff whenever C in E
refines ff whenever C in E
Reference 
- Junnila, Heikki J.K. and Künzi, Hans-Peter A., Ortho-bases and monotonic properties.,[J] Proc. Am. Math. Soc. 119, No.4, 1335-1345 (1993).
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ