Definition 1 
A topological space is called semicompact if every semiopen cover has a finite subcover.
Definition 2 
Same as locally peripherally compact.
Property 
The following properties are all for Definition 1.
- [Dorsett1981] A space is semicompact iff it satisfies the following.
- [Ganster1987] A space X is semicompact iff it satisfies the following.
- X is S-closed.
- For every infinite subset S,
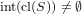 .
.
Reference 
- Definition 1
- Dorsett, Ch. Semi-compact R1 and product spaces, Bull. Malaysian Math. Soc., 3(2) (1980), 15-19.
- Ch. Dorsett, Semi compactness, semi separation axioms, and product spaces, Bull. Malaysian Math. Soc. (2) 4 (1981), 21-28.
- M. Ganster, Some remarks on strongly compact spaces and semi compact spaces, Bull. Malaysian Math. Soc. (10) 2 (1987), 67-81.
- Definition 2
- K. Morita, On closed mappings. II, Proc. Japan Acad. Vol.33, No.6 (1957) pp.325-327
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ