stably compact

Definition

• A topological space is called stably compact if it is;
  1. T_0
  2. compact;
  3. locally compact;
  4. coherent, that is, intersections of compact saturated sets are compact;
  5. well-filtered, that is, if the intersection of a filter base 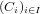of compact saturated sets is contained in an open set, then so is some C_i already.

Reference

• Achim Jung and M. Andrew Moshier, On the bitopological nature of Stone duality (2006)