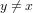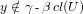γ-βT_2

Definition

• A topological space (X,τ) with an operation γ on τ is called γ-βT_2 if and only if for each pair of distinct points x, y in X, there exists two disjoint γ-β-open sets U and V containing x and y respectively.

Property

• The following are equivalent for a topological space (X,τ) with an operation γ on τ :
  1. X is γ-βT_2.
  2. Let x ∈ X. For each 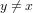, there exists a γ-β-open set U containing x such that .
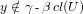  3. For each x ∈ X, ∩{γ-βcl(U) : x ∈ U ∈ γ-βO(X)} = {x}.
• γ-βT_2 ⇒ γ-βT_1.

Reference

• Basu, C. K.; Afsan, B. M. Uzzal; Ghosh, M. K., A class of functions and separation axioms with respect to an operation. (English summary), Hacet. J. Math. Stat. 38 (2009), no. 2, 103–118.