T_1
Last-modified: 2013-04-19 (金) 13:03:31
Definition 
Property 
- A topological space (X,τ) is a T_1 space iff one of the following conditions holds:
- ∀x∈X, {x}' is empty. [5]
- ∀x∈X, cl({x})={x}. [5]
- ∀x,y∈X,
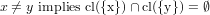 . [5]
. [5]
- Every subset of X is a Λ-set. [7]
- T_1 = T_0 + R_0. [2]
- T_1 = T_R + R_0. [6]
- T_1 = T_0 + C_0. [6]
- T_1 ⇒ nearly T_1. [3]
- T_1 ⇒ T_{EF}. [4]
- T_1 ⇒ λ-T_1. [8]
Reference 
- ???
- Dorsett C., Images and hyperspaces of s-essentially T_1 and s-essentially T_2 spaces and semitopological properties. (Serbo-Croatian summary) Glas. Mat. Ser. III 21(41) (1986), no. 2, 415–422.
- Przemski M., Nearly T_i-continuous functions and some separation axioms. (Serbo-Croatian summary), Glas. Mat. Ser. III 21(41) (1986), no. 2, 431–435.
- McSherry D. M. G. , On separation axioms weaker than T_1. , Proc. Roy. Irish Acad. Sect. A 74 (1974), 115–118.
- Guia Josep, Axioms weaker than R0., (Serbo-Croatian summary), Mat. Vesnik 36 (1984), no. 3, 195-205.
- Guia Josep, Essentially T_D and essentially T_UD spaces., Bull. Math. Soc. Sci. Math. R. S. Roumanie (N.S.) 32(80) (1988), no. 3, 227-233.
- Arenas Francisco G., Dontchev Julian, Ganster Maximilian, On λ-sets and the dual of generalized continuity., Questions Answers Gen. Topology 15 (1997), no. 1, 3-13.
- Caldas Miguel, Jafari Saeid, Navalagi Govindappa, More on λ-closed sets in topological spaces.,Rev. Colombiana Mat. 41 (2007), no. 2, 355-369.


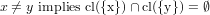 . [5]
. [5]
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ