アルゴリズム勉強会 最短経路問題

Last-modified: 2014-07-09 (水) 20:50:29
 

前回の課題の講評

学内限定
http://www.ugs.kochi-tech.ac.jp/kutpg/internal/contest/algorithm_workshop3/

最短経路問題のアルゴリズムの必要性

アルゴリズム勉強会で前回扱った「深さ優先探索」を用いることで、最短経路を求めることができました。

しかし、深さ優先探索によるアルゴリズムでは、計算量が O(n!) と非常に大きくなり、大きい n (n > 13) に対しては現実的な解法と言えません。

現実の問題として、東京から高知までの陸路での最短経路を求める際に、考えうる頂点 (経由地) n が 13 より小さいはずがなく、O(n!) のアルゴリズムでは話になりません。

そのため、最短経路問題をより高速に解くためのアルゴリズムが必要となります。

最短経路問題のアルゴリズム

最短経路問題を解くアルゴリズムとして、もっと有名と思われるアルゴリズムがダイクストラ (Dijkstra) 法です。
法では、ある頂点から、他のすべての頂点までの最短経路を O(n log n) で求めることができます。

ダイクストラ法以外のアルゴリズムでは、ベルマンフォード (Bellman-Ford) 法やワーシャルフロイド (Warshall-Floyd) 法が有名です。

ダイクストラ法

最短経路問題のアルゴリズムとして、最も使用頻度が高いと思われるダイクストラ法について解説します。
ダイクストラ法では、深さ優先探索とは全く別のアプローチを取って、最適解を求めます。

ダイクストラ法で用いられる手法は、動的計画法 (DP: Dynamic Programming) と呼ばれ、最短経路問題以外でも様々な問題のアルゴリズムに用いられています。*1

次のような無向グラフがあったとします。

 
Graph2.png
 

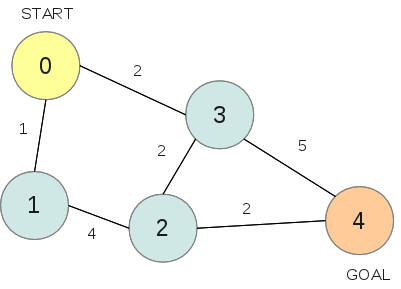
そのようなグラフに対し、ダイクストラ法では次のような表を用意します。

頂点名最短距離確定済み
00F
1infinityF
2infinityF
3infinityF
4infinityF

上記の表は、各頂点までの暫定での最短距離をまとめたものです。
ある地点までの最短距離が最適解であり、今後変更されることがない場合、確定済みとして記憶します。

ダイクストラ法は次のようなステップで進みます。

  1. 開始地点を距離 0 で初期化する。
  2. 表の中で確定済みでない頂点から、最もそこまでの最短距離の短い頂点を選ぶ。
  3. 選んだ頂点を、確定済みとする。
  4. 選んだ頂点から、辺のある頂点の最短距離を更新する (小さくなる場合)。
  5. 確定済みでない頂点が無い場合、アルゴリズムを終了する。ある場合、2 へ戻る。

ダイクストラ法を実装する際のポイントは、頂点を管理する際に、優先順位付きキュー (PriorityQueue) を使うことです。

優先順位付きキューを使うことにより、ステップ 2 がキューから取り出すだけの処理にすることができ、実装がとても簡単になります。

計算量は、ステップ 2 が優先順位付きキューからの取り出しで　O(log n)、ステップ 4 が O(n) なので O(n log n) となります。*2

演習

実際に手作業でやってみましょう。

fileDijkstra.pdf

Java での実装方法

Java でのダイクストラ法の実装例を載せます。

辺の保持

深さ優先探索でやっと時と同様、辺は2次元配列で保持します。
次のような変数 edge を用意し、edge[x][y] を x -> y の重みとします。

int [][] flag = new int[v][v];

ダイクストラ法で使用する表の実装

未確定の頂点を保持するために、優先順位付きキュー (PriorityQueue) を使います。

Queue<T> q = new PriorityQueue<T>();

頂点の情報 T の実装

PriorityQueue に追加する要素には、比較するためのインターフェイス Comparable<T> を実装する必要があります。

class T implements Comparable<T> {
    int i, c;

    T(int i, int c){
        this.i = i;
        this.c = c;
    }

    public int compareTo(T other){
        return this.c - other.c;
    }
}

初期状態の追加

初期状態として、開始地点 a を距離ゼロとしてキューに登録します。

q.offer(new T(a, 0));

確定済み頂点の保持

確定済み頂点を保持するために、1次元配列を使います。

boolean [] flag = new boolean[v];

値の更新処理

キューから頂点が無くなるまで、他の頂点の距離の更新処理を行います。

// キューに未確定頂点がある間
while(!q.isEmpty()){
    T t = q.remove();

    // 確定済みかどうか
    if(flag[t.i]) continue;
    flag[t.i] = true;

    // 終了地点かどうか
    if(t.i == b){
        return t.c;
    }

    // 更新処理
    for(int i = 0; i < v; ++i){
        if(edge[t.i][i] < INF){
            // 今までの距離 + 新規の距離
            q.offer(new T(i, t.c + edge[t.i][i]));
        }
    }
}

課題

KOJ にある問題を解いてください。
O(n log n) で実装できるなら、どのプログラミング言語で実装しても構いません。

問題 URL
http://kut-oj.appspot.com/contest/algorithm_workshop4/

解説, 講評 (学内限定)
http://www.ugs.kochi-tech.ac.jp/kutpg/internal/contest/algorithm_workshop4/

挑戦課題

すべて、ダイクストラ法で解けます。

一番上は、高校生が解く問題なので、大学生であれば当然解けるはずですよね。*3

 
*1 巡回セールスマン問題, ナップザック問題等。
*2 優先順位付きキューを使わないと、O(n^2) となります。
*3 ですよね?