Welcome to Encyclopedia of Separation Axioms

只今工事中。
(それでも見たい方はどうぞ。)
誰も編集する方がいなくなった事もあり,一人でやるならTeXで書いた方が楽なのでここでの更新を放置しています.PDFが欲しい方は作っている人に・・・.(完成したらあげるかもしれません.)
注意事項 
- 当サイトは分離公理(Separation Axiom)を集めたサイトです。
- 分離公理であればsemitopology, fuzzy topology, supra bitopologyだろうが何でも構いません(topologyに関係なくてもよい)。
- 集める対象となるのは何かの文献に載っているか、arXive等のサイトにpreprintとしてあがっているものに限る事とする。
- 順番は辭書式順序にします。
- 出典をかならず明記してください(できたら初出のものが望ましい...です)。
- 性質にも出典を明記すること。但し、出典がReferenceの一番上の場合に限り明示しなくても良い。
- 書式はMenue2のテンプレに準拠する事とする。
- 項目名は省略の無いものを最低1つ作る事とし、省略のある項目には詳細を書かずリンクを張る事とする。
- 公理系は、普通の位相空間に対しては特に断らない限りZFC公理系とする。
- 必ずどのような空間に対する分離公理か明記する事とする。
- neighbourhoodはopenとは限らない。
- 分離公理を探していて図らずも~compactを見つけた場合、Encyclopedia of Compactness
 にお願いします。
にお願いします。 - wikiの仕組みや使い方についてはAbout Wiki等を参照して下さい。
- 気になることがあったら板、編集ノートに書いてください。
Notation 
- ^{\ast}と書くところは*で済ましております。
- 位相空間の記法は基本的に(X, τ_1, τ_2, τ_3,...), (X, τ, μ, ρ,...), (X, T_1, T_2, T_3,...)又は(X, T, S, V,...)に統一します。(X, τ)を単にXと略記することもあります。
- 分離公理T, Rに対してT+RによりTかつRを表すことにする。
- 集合Sのclosureは基本的にcl(S), Cl(S)または
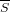 とします。又、内点はint(S), Int(S)または
とします。又、内点はint(S), Int(S)または
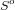 で表わすことにします。
で表わすことにします。 - 位相空間(X, τ)の中の開集合全体の集合をO(X), pre-open set全体の集合をPO(X)、semi-openの場合はSO(X)のように書くことがあります。
- 概ねpreclosureはp-cl(S) , semi-closureはs-cl(S) , α-closureはα-cl(S) にします。
- semi-generalized-open等はsg-openのように略記することもあります。
- P(X)はXの冪集合とする。
- ker(x) は点xのkernelとする。
- {x}' は点xのderived set とする。
List 
A 
- accessible?
- akc?
- almost completely regular
- almost weakly Hausdorff
- almost regular
- anti Hausdorff?
C 
- C_0
- C_D
- C_R
- cnkc?
- collectionwise Hausdorff
- complemented?
- completely Hausdorff?
- completely normal?
- completely normal Hausdorff?
- completely regular?
- completely regular Hausdorff?
D 
F 
G 
H 
- Hausdorff?
J 
- J_0?
K 
M 
- mildly Hausdorff
- MN-p-R_0?
- MN-p-R_1?
N 
- nearly T_1
- nearly T_2
- nearly T_3
- nkc?
- normal (未定義)
- normal Hausdorff?
P 
- pairwise completely normal?
- pairwise completely regular?
- pairwise Hausdorff
- pairwise normal?
- pairwise perfectly normal?
- pairwise R_0 in the sense of Murdeshwar and Naimpally
- pairwise R_1 in the sense of Murdeshwar and Naimpally
- pairwise R_1 in the sense of Reilly
- pairwise regular
- pairwise semi-Hausdorff?
- pairwise T_0 in the sense of Murdeshwar and Naimpally
- pairwise T_1 in the sense of Murdeshwar and Naimpally
- pairwise T_1 in the sense of Reilly
- pairwise T_1 in the sense of Swart
- pairwise T_{1/2}?
- pairwise T_2
- pairwise T_{2 1/2}?
- pairwise T_3
- pairwise T_{3 1/2}?
- pairwise T_4?
- pairwise T_5?
- pairwise Tychonoff?
- pairwise weakly Hausdorff?
- p-D_0?
- p-D_1?
- p-D_2?
- perfectly normal?
- perfectly normal Hausdorff?
- p-regular
- preregular?
- pre-D_0
- pre-D_1
- pre-D_2
- pre-R_0
- pre-R_1?
- presober
- pre-T_0
- pre-T_1
- pre-T_2
- pre-Urysohn
- pre-US
Q 
R 
S 
- S_0?
- S_1?
- S_2?
- s-D_0?
- s-D_1?
- s-D_2?
- semi-D_0
- semi-D_1
- semi-D_2
- seminormal?
- semi-R_0
- semi-R_1
- semiregular?
- semi-T_0
- semi-T_1
- semi-T_{1/2}
- s-essentially T_0
- s-essentially T_1
- s-essentially T_2
- sober
- soft normal
- soft regular
- soft seminormal
- soft semiregular
- soft semi T_0
- soft semi T_1
- soft semi T_2
- soft semi T_3
- soft semi T_4
- soft T_0
- soft T_1
- soft T_2
- soft T_3
- soft T_4
- strong T_0
- strong T_D
- strongly Hausdorff
- strongly R_1
- strongly s-essentially T_0
- strongly semiregular?
- strongly s-regular (未定義)
- submaximal
- symmetric?
T 
- T_0 (要出典)
- T_1 (未定義)
- T_1∨(∖T_{UD})?
- T_{1/2} (未定義)
- T_{1/3}?
- T_{1/4}?
- T_-1
- T_2 (未定義)
- T_{2 1/2}?
- T_3 (未定義)
- T_{3 1/2}?
- T_{3/4}?
- T_4?
- T_5?
- T_6?
- T_a
- T_B?
- T_b
- T_c?
- T_D
- T_d?
- T_{DD}
- T_D∨(∖T_{UD})?
- T_{EF}
- T_{ES}
- T_F
- T_{FD}?
- T_{FF}
- T_G?
- T_H?
- T_{HG}?
- T_{HUD}?
- T_I?
- T_{IUD}?
- T_{IUH}?
- T_J?
- T_K?
- T_{KJ}?
- T_{KUH}?
- T_L?
- T_R
- T_S
- T_{UB}
- T_{UD}
- T_{UH}?
- T_{UI}?
- T_Y
- T_{YS}
- T_α
- T_β
- T^Ω_{1/2}?
- T(i,k)
- T^#_b?
- T^#_c?
- T^#_{1/2}?
- T*_{1/2}?
- Tychonoff?
U 
W 
- w-C_0
- w-R_0?
- weakly C_0?
- weakly Hausdorff
- weakly mildly Hausdorff
- weakly pairwise Hausdorff?
- weakly pairwise T_3?
- weakly pairwise T_{3 1/2}?
- weakly pairwise T_4?
- weakly pre-R_0
- weakly R_0
- weakly semi-R_0
- weakly submaximal
- weakly α-R_0?
- W-p-T_2?
- W-p-T_3?
- W-p-T_{3 1/2}?
- W-p-T_4?
ギリシャ文字 
- α-D_0?
- α-D_1?
- α-D_2?
- α-R_0?
- α-R_1?
- α-symmetric?
- α-T_0
- α-T_1
- α-T_2
- _αT_b?
- _αT_c?
- _αT_{αgs}?
- β*T_1/2?
- β**T_{1/2}
- γ-β-normal
- γ-β-regular
- γ-βT_0
- γ-βT_1
- γ-βT_{1/2}
- γ-βT_2
- Λ^s_δ-D_0
- Λ^s_δ-D_1
- Λ^s_δ-D_2
- Λ^s_δ-symmetric
- λ-D_0
- λ-D_1
- λ-D_2
- λ-R_0
- λ-R_1
- λ-T_0
- λ-T_1
- λ-T_{1/2}
- λ-T_2
- ^ΩT_{1/2}?
記号 
- (1, 2)*pre-D_0?
- (1, 2)*pre-D_1?
- (1, 2)*pre-D_2?
- (1, 2)*pre-regular?
- (1, 2)*pre-T_0?
- (1, 2)*pre-T_1?
- (1, 2)*pre-T_2?
- (i, j)-almost completely regular?
- (i, j)-almost normal?
- (i, j)-almost regular?
- (i, j)-completely regular?
- (i, j)-D_1?
- (i, j)-seminormal?
- (i, j)-semi regular
- (i, j)-regular?
- (α, α)-T_{1/2}?
- ^#T_b?
- ^#T_c?
- ^#T_{1/2}?
- <λ-collectionwise Hausdorff
- ≦λ-collectionwise Hausdorff
用語の補足 
- absolute complement
- closed discrete collection
- compact
- degenerate
- derived set
- essential degenerate
- essential derived set
- generalized closed
- generalized open?
- generic point
- intersection of soft sets
- irreducible
- kernel
- operation
- p-convergence
- pD-set?
- pre-open?
- pre-Difference set
- pre-semi-closed function
- reducible
- regular open
- regular with respect to τ?
- relative complement
- relative complement(soft)
- screened
- sD-set?
- semi-Difference set
- semi-kernel of x
- semi-closed
- semi-closure
- semi-generalized closed
- semi-generalized open
- semi-open
- semi star generalized closed
- semi-T_0-identification space of (X,τ)
- separated (要出典)
- separated by neighbourhoods (要出典)
- soft closed
- soft closure
- soft interior
- soft open
- soft point
- soft semiclosed
- soft semiopen
- soft set
- soft subset
- soft topological space
- soft topology
- star of the point x with respect to U
- T_1-open cover
- T_2-open cover
- T_3-open cover
- topologically distinguishable (要出典)
- topologically indistinguishable (要出典)
- ultraseparated
- union of soft sets
- weakly separated
- α-open?
- α-set
- β-closed
- β-closure
- β-interior
- β-open
- β*g-closed
- β*-set
- γ-closed
- γ-closure?
- γ-interior?
- γ-open
- γ-β generalized closed
- γ-β generalized open
- γ-β-open
- γ-β-closed
- δ-closed
- δ-interior
- δ-open
- δ-semiclosed
- δ-semiopen
- δ-Λ_s-semiclosed
- η-closed
- η-open
- Λ^s_δ-D set
- Λ^s_δ-neat point
- Λ^s_δ-set
- (Λ,sδ)-closed
- (Λ,sδ)-closure
- (Λ,sδ)-cluster point
- (Λ,sδ)-open
- (Λ,sδ)-property
- Λ-set
- λ-closed
- λ-closure
- λ-cluster point
- λ-Difference set
- λ-open
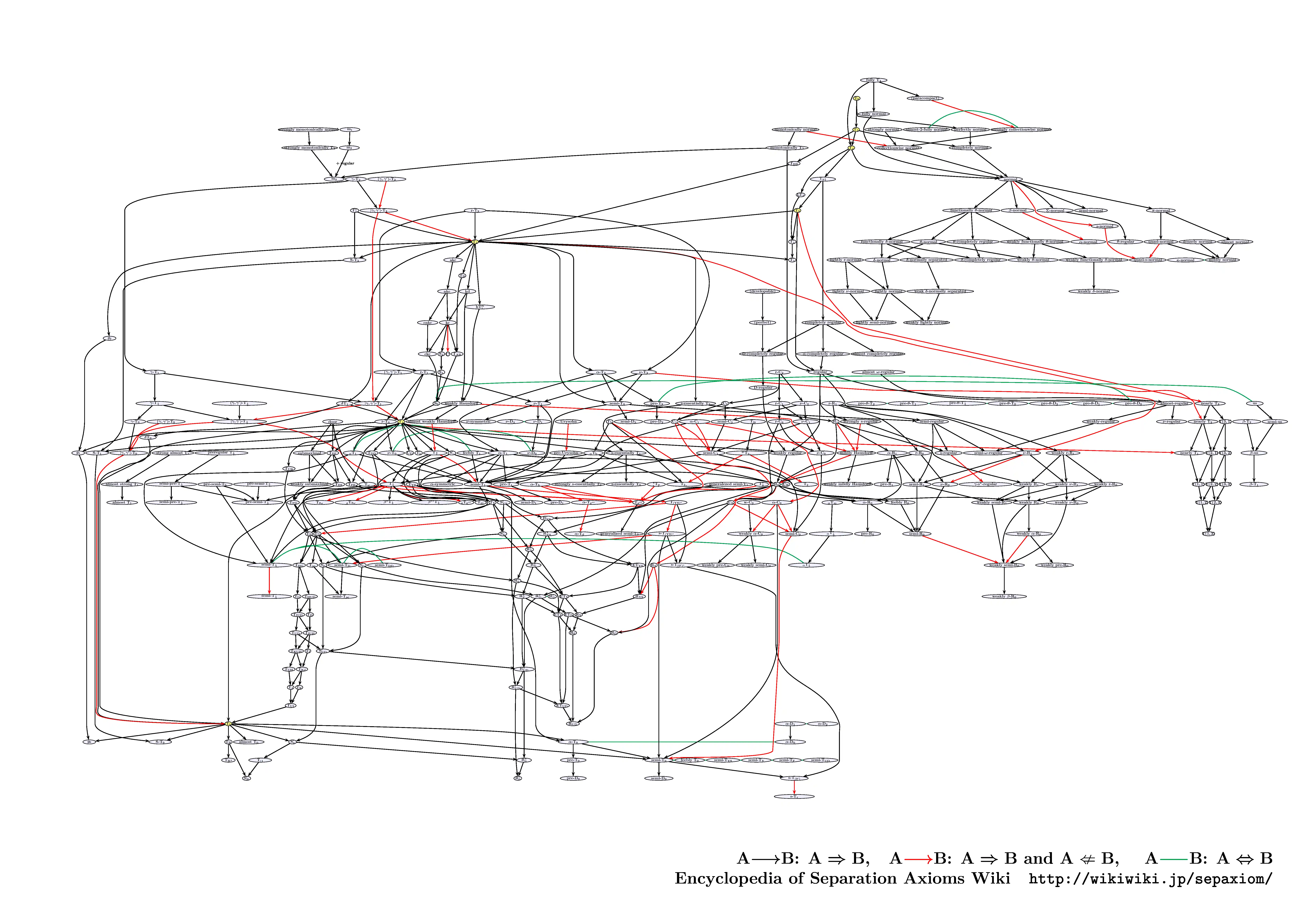
Relation 
分離公理の関係の図です。(一部のブラウザでは表示されないかもしれません。)
いろいろ整理されていませんがご了承ください。また、このグラフはかなり途中段階の物ですが悪しからず。
このグラフは証明を全部おって作っているわけではありません。なるべく間違いがないように気をつけていますが、論文が間違えている場合そのまま反映されることがありますので、怪しい点は自分で確かめてください。
同じ名前の違う定義があるものは片方の名前を少しいじっています。
技術協力戴いたH7K, monae両氏にこの場を借りて改めて感謝申し上げます。
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ