R_0
Last-modified: 2011-07-10 (日) 18:18:23
Definition 
Property 
- A topological space (X, τ) is R_0 if it satisfies one of the following equivalent conditions:
-
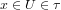 implies
implies
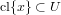 .
.
- cl({x})=∩{U | U is an open neighbourhood of x} for each x in X.
- cl({x})=cl({y}) or cl({x}) ⋂ cl({y})=
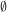 for x, y in X.
for x, y in X.
- The specialization preoreder? on X is symmetric?.
- The fixed ultrafilter at x convereges only to the points that x is topologically indistinguishable from.
- The Kolmogorov quotient? of X ( which identifies topologically indistinguishable points) is T_1
- Every open set is the union of closed sets.
- A topological space (X,τ) is R_0 iff for any point x in X, cl({x}) ⊆ ker(x).
- An R_0 space is a w-R_0 space. The converse does not hold.
- R_0 ⇒ C_0. [4]
- R_0 ⇒ R_T. [2]
- R_0 ⇒ R_YS?. [3]
- R_0 ⇒ R_D. [3]
- R_0 ⇒ R*_D. [4]
- R_0 + normal ⇒ regular. [3]
Reference 
- 忘れた。
- Tong, Jing Cheng, On the separation axiom R0. (Serbo-Croatian summary), Glas. Mat. Ser. III 18(38) (1983), no. 1, 149–152.
- Misra, D. N.; Dube, K. K., Some axioms weaker than the R0-axiom., (Serbo-Croatian summary), Glasnik Mat. Ser. III 8(28) (1973), 145-148.
- Guia, Josep, Essentially T_D and essentially T_UD spaces., Bull. Math. Soc. Sci. Math. R. S. Roumanie (N.S.) 32(80) (1988), no. 3, 227-233.


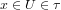 implies
implies
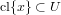 .
.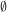 for x, y in X.
for x, y in X.
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ