w-C_0
Last-modified: 2011-05-29 (日) 13:42:30
Definition 
- A topological space (X,τ) is said to be w-C_0 if
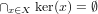 .
.
Remark 
Property 
- A topological space (X,τ) is w-C_0 iff for each x in X, there exists a proper closed set C such that x in C, i.e. iff for each x in X, cl({x}) ≠ X.
- If a space X is w-C_0, then for every topological space Y, the product space X×Y is also w-C_0.
- If a product X×Y is w-C_0, the at least one of the factor is w-C_0.
Reference 
- Di Maio, Giuseppe, A separation axiom weaker than R0. (English) [J] Indian J. Pure Appl. Math. 16, 373-375 (1985).




 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ