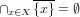weakly R_0

Last-modified: 2011-05-29 (日) 14:50:31

Definition

  • Let (X,τ)　be a topological space. X is said to be weakly R_0 , briefly w-R_0 , if imgtex.fcgi?%5bres=100%5d%7b%5c%5b%20%5ccap_%7bx%5cin%20X%7d%5coverline%7b%5c%7bx%5c%7d%7d=%5cemptyset%20%5c%5d%7d%25.png .

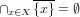Property

  • A topological space (X,τ) is weakly-R_0 iff for each x in X, ker(x) ≠ X.
  • If a space X is w-R_0, then for every topological space Y, the product space X×Y is also w-R_0.
  • If a product X×Y is w-R_0, the at least one of the factor is w-R_0.
  • weakly R_0 ⇒ weakly semi-R_0. [2]

Reference

  1. Di Maio, Giuseppe, A separation axiom weaker than R0., (English) [J] Indian J. Pure Appl. Math. 16, 373-375 (1985).
  2. Arya, S.P.; Nour, T.M., Weakly semi-R_0 spaces., (English) [J] Indian J. Pure Appl. Math. 21, No.12, 1083-1085 (1990).