Definition 1 
A topological space is said to be C-compact (abbreviated as CC) if every closed set is an H-set.
Definition 2 
For subspaces of topological spaces, C-compactness is the same as C_ω-compactness. Here ω denotes countable cardinality.
Definition 3 
A topological space is called c-compact if for every topological space Y and every subset
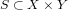 ,
,
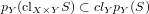 , where
, where
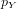 is the second projection
is the second projection
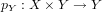 .
.
Remark 
- Definition 1
- G. Viglino, C-compact spaces. Duke Math. J., 36, 761-764 (1969).
- R.F. Dickman, Jr. and J.R. Porter, Between minimal Hausdorff and compact Hausdorff spaces, Topology Proc. Vol.9 (1984), p.243-268.
- Definition 2
- Manuel Sanchis, Angel Tamariz-Mascarua, p-pseudocompactness and related topics in topological spaces, Topology and its Applications 98 (1999) 323-343.
- Definition 3
- C. M. Neira, The Kuratowski-Mrowka characterization and weak forms of compactness, Revista Colombiana de Matematicas Volumen 43(2009)1, paginas 9-17
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ