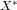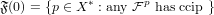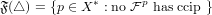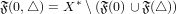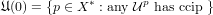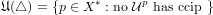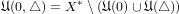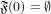Definition 
A Tychonoff space X is called wa-realcompact if for every
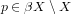 , there is a decreasing sequence
, there is a decreasing sequence
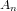 of closed subsets in X which satisfies
of closed subsets in X which satisfies
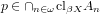 and
and
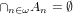 .
.
Remark 
Let
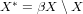 . For
. For
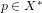 ,
,
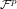 (
(
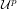 ) denotes the set of all free closed (resp. open) ultrafilters on X converging to p.
) denotes the set of all free closed (resp. open) ultrafilters on X converging to p.
Similarly, we introduce the following devision;
(cf. ccip).
Then generalization of realcompactness is characterized as following;
- X is almost realcompact iff
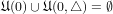 ;
; - X is c-realcompact iff
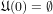 ;
; - X is a-realcompact iff
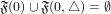 .
.
WA-realcompactness is introduced from this results so that
See [Isikawa] for details.
Reference 
T. Isiwata, Closed ultrafilters and realcompactness, Pacific J. Math. 94 (1981) 68-71.
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ