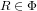Definition 
- a compact space X is Dugundji if it has one of the following equivalent properties:
- if Z is a zero-dimensional compact space and A is a closed subset of Z, then
every continuous map A → X extends to a continuous map Z → X; - there exists a family Φ of closed equivalence relations on X such that:
- if Z is a zero-dimensional compact space and A is a closed subset of Z, then
Property 
- For every topological group X every compact G_δ-subset of X is Dugundji.
- For every Mul’tsetv space? X every compact G_δ-subspace of X is Dugundji.
Reference 
- Reznichenko, E. A.(RS-MOSCM-GT) and Uspenskij, V. V.(RS-MOSCM-GT), Pseudocompact Malʹtsev spaces. (English summary) ,Special issue on topological groups. ,Topology Appl. 86 (1998), no. 1, 83--104.
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ