Rosenthal-Banach compact
Last-modified: 2010-08-30 (月) 23:24:27
Definition 
- A compact Hausdorff set K is called Rosenthal-Banach compact, if there is a polish space X and a Banach space E so that K is homeomorphic with a compact subset of B_1(X,E) in the topology of pointwise-weak convergence?, where B_1(X,E) is the set of functions which there is a sequence
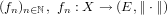 continuous for every n ∈ N, such that if t ∈ X then
continuous for every n ∈ N, such that if t ∈ X then
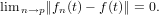
Property 
Reference 
- Mercourakis, S. and Stamati, E., Compactness in the first Baire class and Baire-1 operators. Serdica Math. J. 28 (2002), no. 1, 1--36.

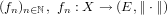 continuous for every n ∈ N, such that if t ∈ X then
continuous for every n ∈ N, such that if t ∈ X then
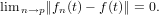


 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ