Definition 
A quasi-uniform space X is almost precompact provided that if U is an entourage, there is a finite subset F of X such that X = cl(U[F]).
Property 
- A quasi-uniform space is almost precompact iff every open ultrafilter on X is a Cauchy filter?.
- A Hausdorff space X is almost-compact iff every compatible quasi-uniformity for X is almost complete and almost precompact.
- (The Generalized Niemytzki-Tychonoff theorem) A Hausdorff space is almost-compact iff it is almost complete with respect to every compatible quasi-uniformity.
- Let
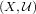 be an almost precompact quasi-uniform space and let
be an almost precompact quasi-uniform space and let
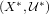 be a regular completion of
be a regular completion of
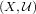 . Then
. Then
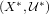 is compact.
is compact.
Remark 
- See almost-compact.
Reference 
P. Fletcher and S. Naimpally, On almost complete and almost precompact quasi-uniform spaces, Czechoslovak Math. J., Vol.21 (1971), No.3, pp.383-390.
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ