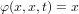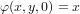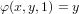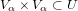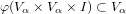Definition 
A Hausdorff space X is called equi-locally convex (ELCX) if there exists an open neighborhood U of the diagonal
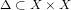 , a mapping
, a mapping
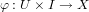 and an open cover
and an open cover
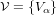 of X such that:
of X such that:
A subset W in X is called convex if
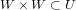 and
and
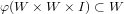 .
.
The cover
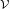 is called a convex open cover of X.
is called a convex open cover of X.
An ELCX space is called coparacompact if any open cover has a locally finite convex refinement.
Reference 
Vladimir P. Okhezin, On the fixed-point theory for non-compact maps and spaces.I, Topological Methods in Nonlinear Analysis, Journal of the Juliusz Schauder Center, Volume 5, 1995, 83-100.
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ