Definition 
- Let M be a subset of a linear topological space X. M is called mean compact if given any sequence
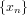 in M there is a point x in X such that
in M there is a point x in X such that
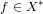 implies
implies
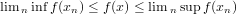 .
.
Reference 
- Heron Sherwood Collins, Completeness and Compactness in Linear Topological Spaces, Transactions of the American Mathematical Society, Vol. 79, No. 1 (May, 1955), pp.256-280.
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ