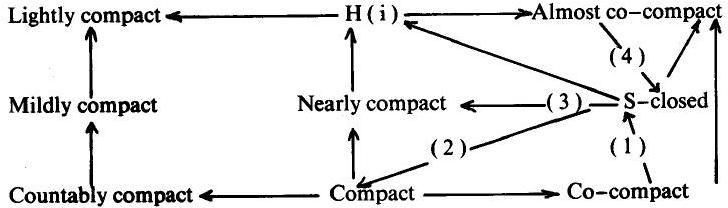
Definition 1 
A topological space X is mildly compact if any countable open cover of X has a finite subfamily the interiors of the closures of whose members cover X.
Property 
Reference 
Abd El-Monsef, M. E.(ET-TANT) and Kozae, A. M.(ET-TANT),Remarks on $s$-closed spaces (Arabic summary), Qatar Univ. Sci. Bull. 6 (1986), 11--21.
Definition 2 
A topological space X is called mildly compact if every clopen cover has a finite subcover.
Reference 
R. Staum, The algebra of bounded continuous functions into a nonarchimedean field, Pacific J. Math., 50 (1974), 169-185.
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ