Definition 
p denotes a free ultrafilter on ω, the set of natural numbers.
Let X be a topological space, (S_n) a sequence of nonempty subsets in X. A point x in X is called a p-limit point of (S_n) if for all neighborhood V of x,
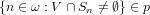 .
.
If (x_n) is a sequence of points in X, "a p-limit point of (x_n)" means a p-limit point of a sequence of singleton ({x_n}).
X is said to be p-compact if every sequence (x_n) has a p-limit point.
Remark 
- If X is p-compact for all p, X is called ultracompact.
- For the term in bitopology, see p-compact in bitopology.
Reference 
- A. R. Bernstein, A new kind of compactness for topological spaces, Fund.Math. 66 (1970), 185-193.
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ