realcompact

Definition

A Tychonoff space is called realcompact if every ultrafilter of zero sets with cip is fixed?.

Property

• A space is realcompact if and only if it is homeomorphic to a closed subspace of a product of real lines.
• Every Tychonoff Lindeloef space is realcompact.
• If X is a Tychonoff space, the following conditions are equivalent:
  1. X is realcompact;
  2. X is the intersection of all cozero sets in the Stone-Cech compactification of X;
  3. X is the intersection of all σ-compact subspaces of the Stone-Cech compactification of X;
  4. every maximal cozero cover has a countable subcover;
  5. if A is a stable family of closed subsets in X with fip, A has a nonempty intersection.
• The image under a perfect mapping of a normal realcompact space is also a realcompact space.
• Realcompact implies both almost realcompact and almost* realcompact.
• X is realcompact iff for each point p in βX-X, there exists a continuous function f on βX such that f(p)=0 and f is positive on X (where βX denotes the Stone-Cech compactification).
• If C_ρ(X) represents the collection of continuous functions with realcompact support, then X is realcompact iff C_ρ(X) = C(X).
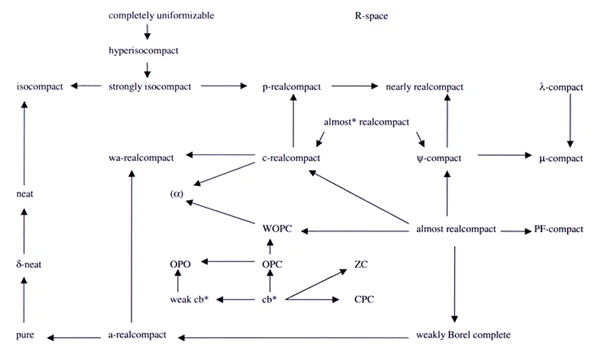
• See the following figure for implication between the related properties.
  

Reference

• Zdenek Frolik, A generalization of realcompact spaces, Czechoslovak Mathematical Journal, Vol.13 (1963), No. 1, 127-138.
• John J. Schommer and Mary Anne Swardson, Almost realcompactness, Commentationes Mathematicae Universitatis Carolinae, Vol.2 (2001), No.2, 383-392.
• Nancy Dykes, Generalizations of Realcompact Spaces, Pacific Journal of Mathematics Vol. 33, No.3, 1970.
• K.P.Hart, J. Nagata and J.E. Vaughan, Encyclopedia of general topology, Elsevier Science.
• M. Mandelker, Supports of continuous functions, Trans, Amer. Math. Soc, 156 (1971), 73-83.
• http://www.utm.edu/staff/jschomme/realcom.html