Definition 
A subset A of a topological space X is called relatively realcompact in X iff
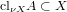 , where νX denotes the Hewitt realcompactification of X.
, where νX denotes the Hewitt realcompactification of X.
Remark 
- Recall that A is relatively compact? in X iff
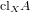 is compact, and that A is relatively pseudocompact in X iff
is compact, and that A is relatively pseudocompact in X iff
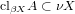 .
. - Note that if A is relatively realcompact in X, the closure of A in X is realcompact space. However, the converse is not true.
Reference 
- J. J. Shommer, Relatively realcompact sets and nearly pseudocompact spaces, Comment. Math. Univ. Calorin. 34,2 (1993) 375-382.
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ