Definition 
A T_1 space X is called superparacompact if every open cover has an open finite component refinement.
Property 
Let X be a completely regular space and let
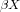 be its Stone-Cech compactification. X is superparacompact iff for every compact
be its Stone-Cech compactification. X is superparacompact iff for every compact
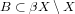 , there exists a finite component cover
, there exists a finite component cover
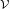 of the space X such that
of the space X such that
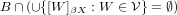 , where
, where
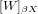 denotes the closure of W in
denotes the closure of W in
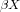 .
.
Reference 
- D. Buhagiar and T. Miwa, On superparacompact and Lindeloef GO-spaces, Houston J. Math. Vol.24, No.3, 1998.
- D. Buhagiar, T. Miwa, and B. A. Pasynkov, Superparacompact type properties, Yokohama Math. J. Vol.46, pp.71-86, 1998.
 新規
新規 編集
編集 添付
添付 一覧
一覧 最終更新
最終更新 差分
差分 バックアップ
バックアップ 凍結
凍結 複製
複製 名前変更
名前変更 ヘルプ
ヘルプ