相関と回帰
散布図
原因と結果の関係を見える化する、2変数の関連性を明らかにするものが散布図であり、横軸に原因を縦軸に結果を対応させる。散布図を用いることで、相関を視覚的に見える化することができ、異常値の発見が容易にできる。また、層別する際にも視覚的に傾向を掴むことができる。
ただし、ここで2変数は連続データ(計量値)であり、それぞれが正規分布に従っていることが条件となる。
ここで、関連性があるかないかを数値で示すものとして、「ピアソンの相関係数」を用いる。
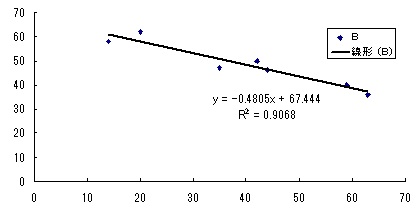
図1 散布図の例
r=1.0で相関あり、r=0.5で相関がありそう、r=0.0で無相関であると言える。r=0.5の場合、検定を行って相関があるか確認する必要がある。また、散布図は層別を行っていない場合と、層別を行ってからでは相関に差がうまれる。
外れ値(異常値)がある場合は正確な相関を求めることができない。値が、異常値か判断するには散布図を確認し、μ±3σを超えているかで判断する。
相関係数の検定
相関係数の有意性について、統計的に相関があるか結論を出す必要があり、仮説を設定する。
[相関に関する検定]
(1)仮説の設定H0:ρ=0(両特性間に相関係数なし
(2)n組のデータから相関係数を求める
(3)r表から判定値r1-0.05/2(n-2)=r0.975(n-2)を読み取る。
(P=0.05、f=n-2)
(4)r>r0.975(n-2)ならば正の相関、r<-r0.975(n-2)ならば負の相関がある。
小林和広氏 島根大学生物資源科学部
ttp://www.ipc.shimane-u.ac.jp/food/kobayasi/index.html