semi-θ-closed

Definition

Let A be a subset of a topological space X.
The intersection of all semiclosed sets containing A is called semi-closure of A (denoted by sCl(A)).
By 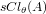we denote the set of all x in X such that 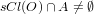for every semiopen set O of X containing x (called semi-θ-closure of A).
A is called semi-θ-closed if .
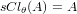The complement of a semi-θ-closed is called semi-θ-open.

Reference

M. Caldas, M. Ganster, D. N. Georgiou, S. Jafari, V. Popa, On a Generalization of Closed Sets, Kyungpook Math. J. 47(2007), 155-164.