Commutatorの基礎理論

この記事はSpeedcubing Advent Calender 2015の25日目の記事として作成されました。

Commutatorの基礎理論

Commutatorの基礎的な部分について、実例を交えながら解説します。
作成に当たってここの内容を基にしています。興味のある方はこちらもどうぞ。

解説の前に

長い記事です。大体の内容は下のまとめに書いてありますので参考にしてください。
画像はクリックで表示、拡大します。
キューブを手元に置いて、実際に回しながら読むことをお勧めします。
徐々に用語が増えるので最初から順番に読んでいくことをお勧めします。
一読してすぐに理解できるような内容ではありませんので、わからなくても嘆く必要はありません。何度でも読み返しましょう。メモとか取りましょう。一発で理解できるのは元からキューブを深く理解している人か、ただの変態です。

まとめ

• Commutatorとは、(手順A)(手順B)(Aの逆手順)(Bの逆手順)の形式をとる手順の総称である。
• Commutatorを使うことで、パーツをある程度思い通りに制御することが出来る。
• Commutatorの影響を受けるのは以下の3領域
  • 「手順Aと手順Bが重なる領域(N)」
  • 「手順AでNに移動する領域(NA')」
  • 「手順BでNに移動する領域(NB')」
• N,NA',NB'が互いに重ならないとき、ABA'B'は(NA'→N→NB')の3点交換を行う。
• Nがパーツ1つなら純粋な3点交換となり、特に便利。
  • ↑Commutatorに慣れてない人はここまででOK
• N=NA' と N=NB' のどちらか1つが成立するパターンも便利。
• その他の場合は必要があったら適宜覚えてください。多分必要ないです。

そもそもCommutatorって何？

Commutatorとは、(手順A)(手順B)(Aの逆手順)(Bの逆手順)の形式をとる手順の総称です。
逆手順を A',B' として、A B A' B'と書きます。
省略表記として [A,B] = A B A' B'が使われます。
逆手順はB A B' A'です。
(例1) [R, U] = R U R' U'
(例2) [R U R', D] = R U R' - D - R U' R' - D'

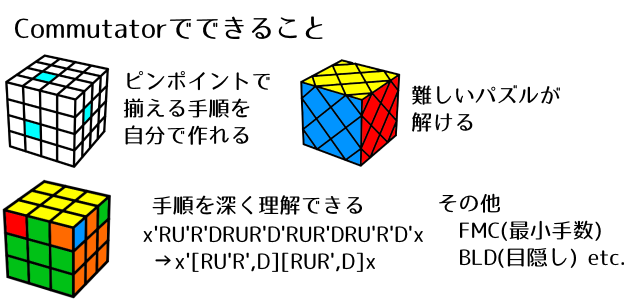
Commutatorって何に使えるの？

Commutatorを使うと、「好きなパーツを」「他のパーツに影響を与えずに」「好きな場所へ」移動させる手順をある程度自由に作り出すことができます。たとえば3x3x3なら、あらゆる3点交換の手順を12手以内で生成できます。*1
ですから、「何に使えるか」と聞かれれば「(工夫次第で)何にでも使える」が答えになります。

4x4x4のセンターだけ移動させたりしたい！
　→Commutatorを使えばそのような手順も自由に作れます。
PLLやOLLは覚えるだけだからつまらないなぁ……
　→Commutatorによって解釈できる手順が意外とあります。手順の理解を深めるのも良いでしょう。
理解を深めてどうすんのさ
　→楽しいじゃん。原理を理解することで、より覚えやすく、かつ忘れにくくなります。
FMC(最小手数競技)がやりたい！
　→重要なテクニックの1つにCommutatorのインサートがあります。
BLD(目隠し)始めるだけなら関係ないよね
　→初心者向けの解法もCommutatorをかじっていれば理解が深まるぞ！
BLDを限界まで速くしたい！
　→じゃあCommutatorだな！(上級者の解法は基本的にCommutatorです)
何このパズル難しすぎ解けないんだけど
　→じゃあCommutatorだな！(このwikiの解法の多くにCommutatorが使われています)

このように、実はCommutatorはキューブ界に深く根を下ろしており誰でもその恩恵を受けることが出来ます。*2タイムの早い遅いや頭の良い悪いは関係ありません。手順をこねくり回すだけなら速さは必要ありませんし、頭が悪いのならじっくり時間をかければいいのです。まずはこのページを読んでみてください。Commutatorを少しでも理解することで、あなたのキューブライフがより豊かなものになることでしょう。なんか自己啓発セミナーみたいですね。

Commutatorではどこが崩れる？

説明をスムースに行うため、以下の用語を定義します。
バンバン使うのでしっかり頭に入れておきましょう。

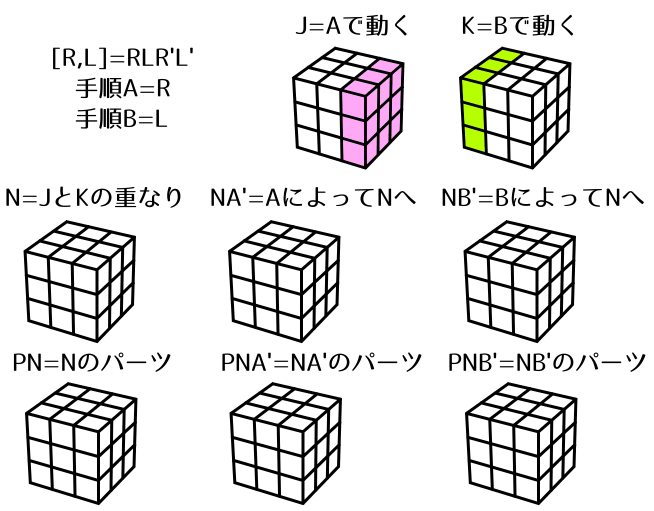
• J……A手順によって動く領域
• K……B手順によって動く領域
• N……JとKの重なる領域
• NA'…A手順によってNへ移動する領域
• NB'…B手順によってNへ移動する領域
• PN……もともとNに存在していたパーツ
• PNA'…もともとNA'に存在していたパーツ
• PNB'…もともとNB'に存在していたパーツ

これらの領域は互いに重なっていても構いません。

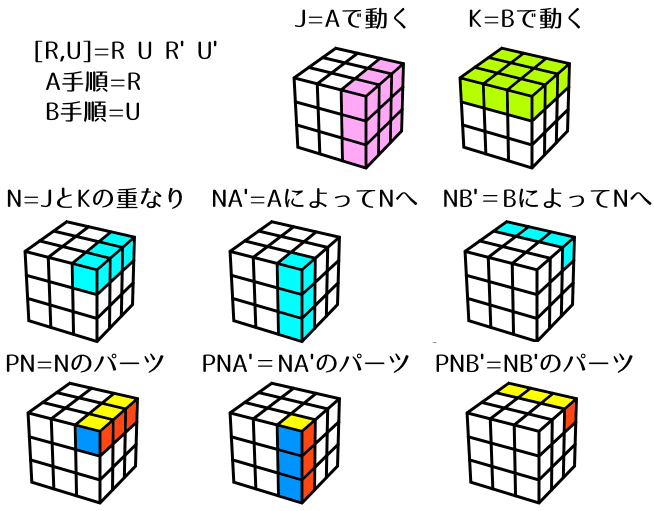
[R,U] = R U R' U' の場合を考えてみましょう。

• A手順はRなので図のピンクの領域(R面)が動きます。ここがJです。
• B手順はUなので緑の領域(U面)が回ります。ここがKです。
• この2つが重なる領域(UBR,UR,UFR)がNです。
• A手順(=R)によってNへ移動する領域(URF,FR,DFR)がNA'です。
• B手順(=U)によってNへ移動する領域(URB,UB,ULB)がNB'です。

これらはただの領域なので、Commutatorの実行中に位置が変化することはありません。

Commutatorの実行前にN,NA',NB'に入っているパーツについて、先頭にPを付けてPN,PNA',PNB'と名前を付けます。
これらはパーツなので、Commutatorの実行中に位置がどんどん変化します。

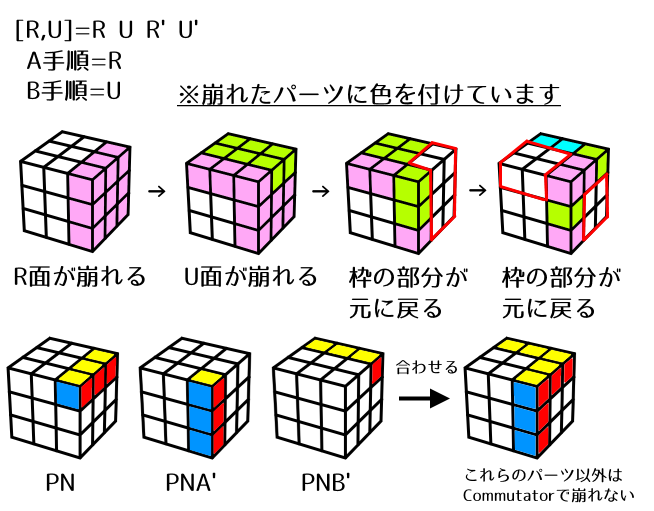
ではまず、Commutatorがどこを崩さないかを考えてみましょう。

• まず、手順A(=R)によってピンクの領域(J)が動きます。
• 次に、手順B(=U)によって緑の領域(K)が動きます。
• その次に手順A'(=R')を行うと、「手順Bによって崩れていない部分」のR面のパーツが正しい位置に戻ります。
• 最後に手順B'(=U')を行うと、「手順A'によって崩れていない部分」のU面のパーツが正しい位置に戻ります。また、PNのうち手順A(=R)によって手順B(=U)から逃れていたパーツ(PNの一部)が崩れます。

このように、JやKのうちNに来ないパーツ(PN,PNA',PNB'のどれでもないパーツ)はAやBで一旦崩れてもA'やB'で元の位置に戻るのでCommutatorの影響を受けません。

よって、Comutatorの影響を受ける可能性があるのは以下の3領域であることがわかります。(超重要)

1. 「手順Aと手順Bが重なる領域(N)」
2. 「手順AでNに移動する領域(NA')」
3. 「手順BでNに移動する領域(NB')」

これからはこれらの領域についてのみ考察をしていきます。

では次に、最もよく使われるCommutatorについて見てみましょう。

最もよく使われるCommutator

N,NA',NB'が互いにどこも重ならないCommutatorが一番よく使われています。ホントもうこれだけ覚えれば帰っていいと思います。
N,NA',NB'はすべて同じ大きさの領域*3なので、Nを1パーツにすると純粋な3点交換手順が作れます。非常に便利です。*4
何が何だかよくわからないと思うので、実例を見てみましょう。

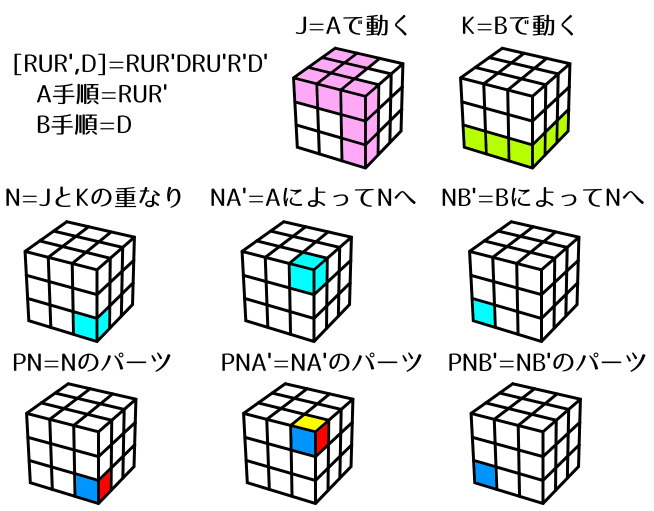
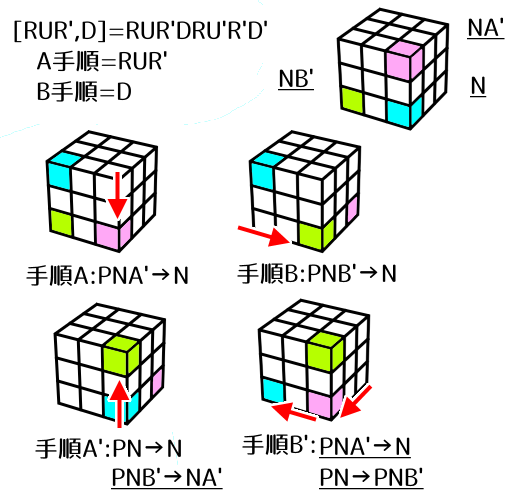
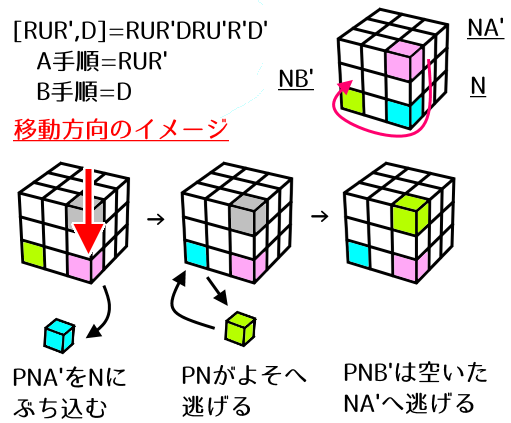
[R U R', D] = R U R' - D - R U' R' - D'
図の通り、N,NA',NB'は互いにどこも重ならず、Nが1パーツになっています。

• 手順A(=R U R')によってNA'にあったPNA'がNへ移動します。PNは一旦Nから追い出されます。
• 手順B(=D)によってNB'にあったPNB'がNへ移動します。今度はPNA'がNから一旦追い出されます。
• 次に手順A'(=R U' R')を行うと、PNB'がNA'へ移動します。同時に、Nを追い出されていたPNがNへ戻ります。
  (手順AによってNを追い出されていたのですから、手順A'を行えばNに帰ってくるのは当然ですね。)
• 最後に手順B'(=D')を行うと、PNがNB'へ移動します。先ほどと同様に、Nを追い出されていたPNA'がPNへ戻ります。
  (手順BによってNを追い出されていたのですから、手順B'を行えばNに帰ってくるのは当然ですね。)

よって、このタイプのCommutatorでは必ず(PNA'→PN→PNB')の3点交換が行われます。
今回はPNA'=RUF,PN=DRF,PNB'=DFLなので、(RUF→DRF→DFL)です。
A手順でNにパーツを叩き込む方向に3点交換が回るイメージです。

他にも例を見てみましょう。

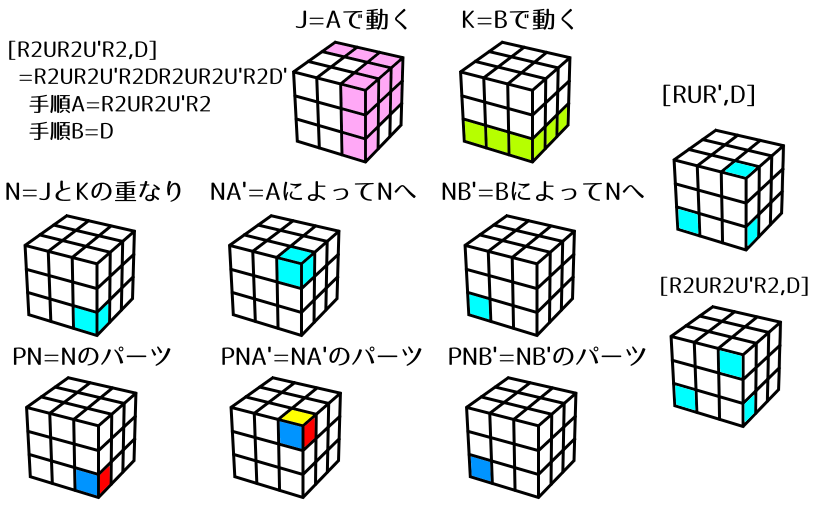
[R2 U R2 U' R2,D] = R2 U R2 U' R2 D R2 U R2 U' R2 D'
PNA'=UFR,PN=DRF,PNB'=DFLなので、3点交換は(UFR→DRF→DFL)です。
先ほどの3点交換と動くパーツは同じですが、向きが少し違います。慣れればこのような向きの調整も自由自在です。詳しいことはこことかを参照してください。

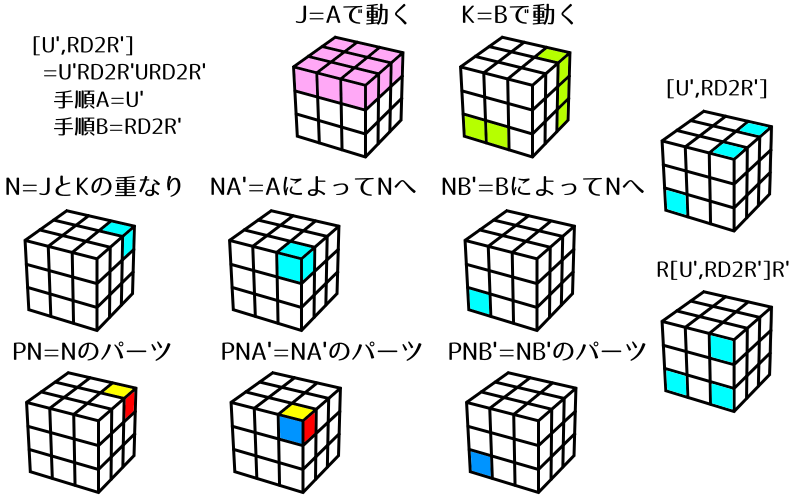
[U',R D2 R'] = U' R D2 R' U R D2 R'
手順Aが短いパターン。
PNA'=UFR,PN=URB,PNB'=FDLなので、3点交換は(UFR→URB→FDL)です。
R D2 R'の部分が、3cycleの解説によく出てくる「すくい上げる」動作です。
ちなみにRのセットアップを付けると、
R - (U' R D2 R' U R D2 R') - R'　→　R U' R D2 R' U R D2 R2
となり、A-permが導けます。

[R' F' R U,R'] = R' F' R U R' U' R' F R2
PNが2パーツあるパターンです。PNがいくつであろうとこのように3点交換できます。
PNA'=(UB,UBL),PN=(UR,URB),PNB'=(RB,RDB)なので、3点交換は(UB,UBL→UR,URB→RB,RDB)です。
ちなみに、RUのセットアップを付けるとU面の2x1x1ブロック3点交換になります。
最後にU'を加えると実質的に2x1x1の2点交換となり、J-permが導けます。
(R U [R' F' R U,R'] U' R') U' = R U R' F' R U R' U' R' F R2 U' R' U'

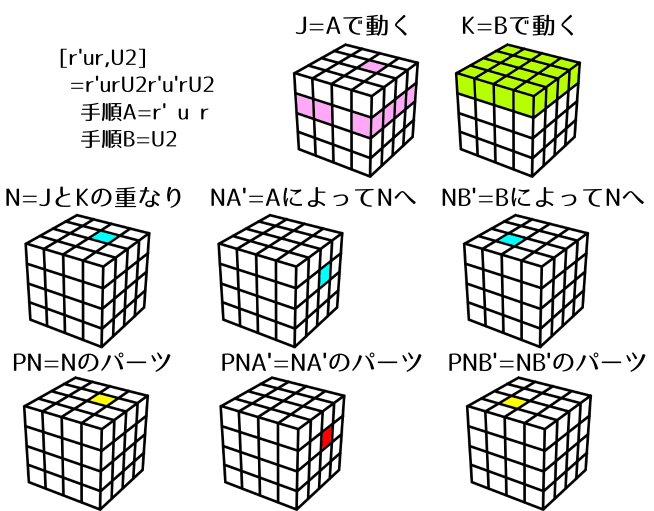
[r' u r,U2] = r' u r U2 r' u' r U2 (4x4x4～)
r’ u r を行うとU面のパーツが1個だけ入れ替わることを利用したCommutatorです。
PNA'=Rbu,PN=Urb,PNB'=Ulfなので、3点交換は(Rbu→Urb→Ulf)です。
多分割だとスライス手順が使いやすいので3x3x3よりCommutatorが作りやすくなる印象があります。

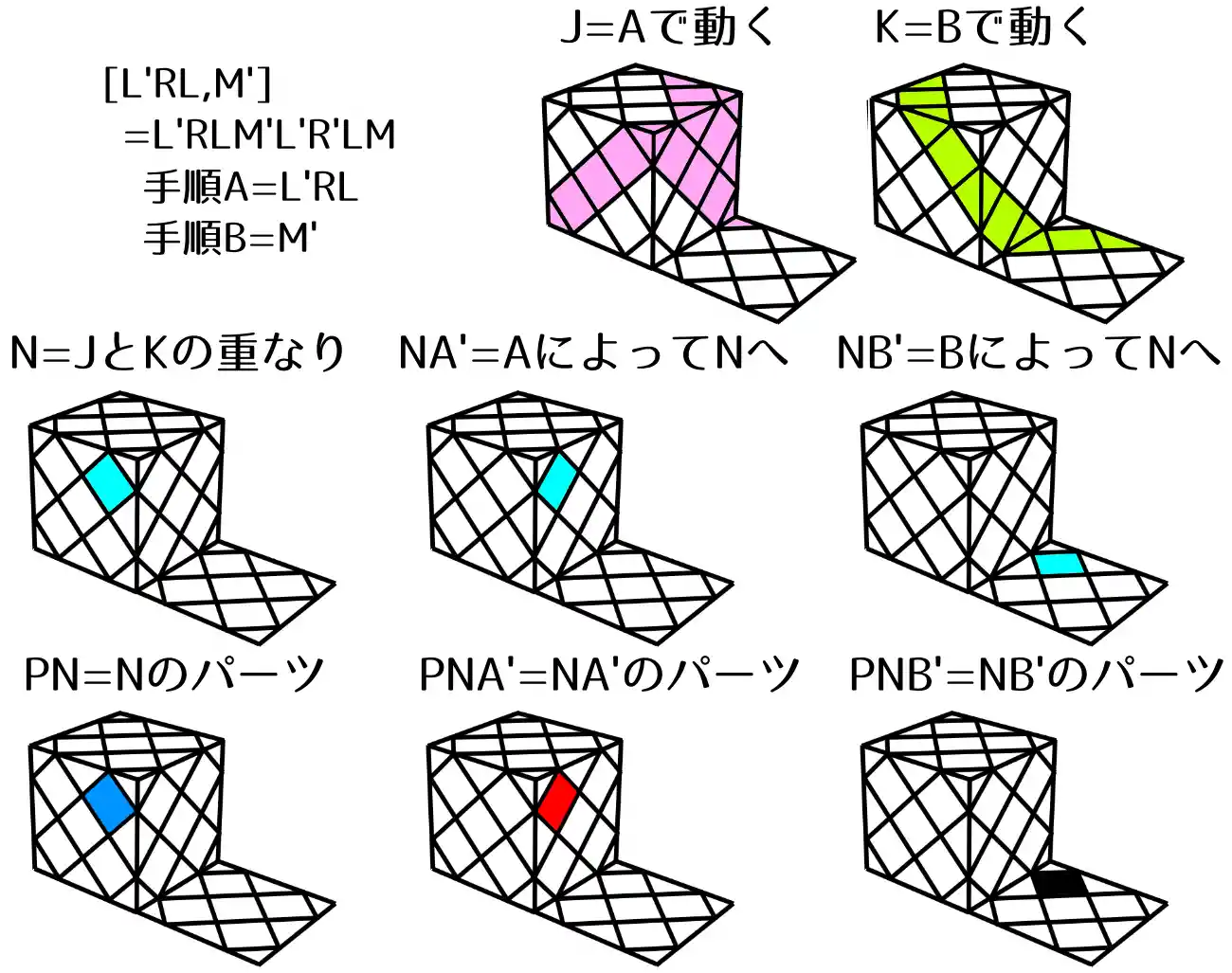
[L' R L,M'] = L' R L M' L' R' L M (Master Skewb)
Master SkewbもCommutatorの手にかかればこの通り。
L' R Lで崩れる領域とM'で崩れる領域が1パーツだけ重なることを利用します。
このような手順の組み合わせを何とかして見つけることがパズル攻略のカギとなることが多いです。この辺は経験や勘がものをいうので、慣れてくるとパズルを見ただけで「これとこれ組み合わせれば解ける」となんとなくわかるようになります。楽しいです。

時々使われるコミュテーター(1)

N=NA'とN=NB'のどちらか一方だけが成立していて、NA'とNB'が重なっていないCommutatorです。
Nを1マスにするとパーツの場所が変化しないので、エッジ反転手順やコーナー回転手順が作れます。Nが2マスであれば、2x2交換手順が作れます。
やっぱり何が何だかよくわからないと思うので、実例を見てみましょう。

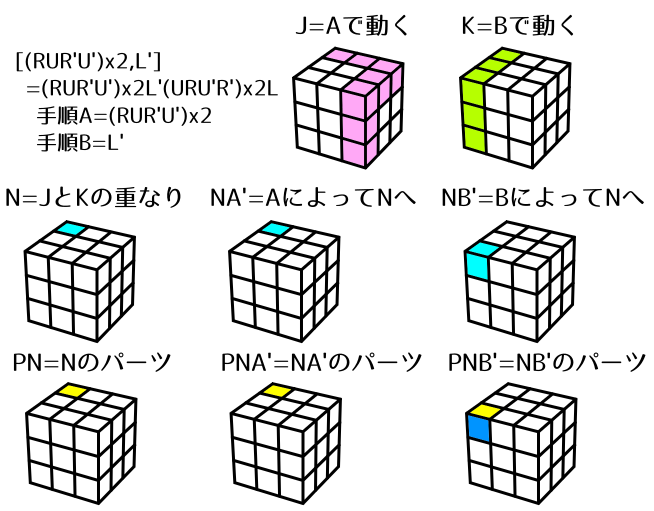
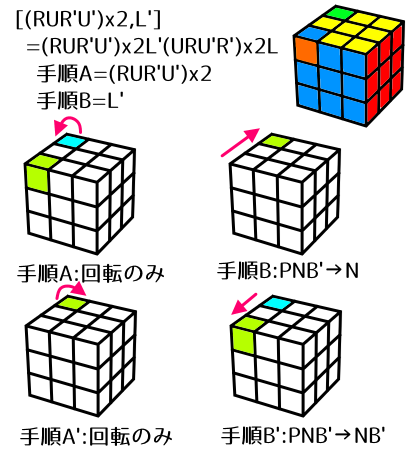
[(R U R' U')x2,L'] = (R U R' U')x2 L' (U R U' R')x2 L

• 手順A(=(R U R' U')x2)によってPNA'はNから移動せず、その場で反時計回りに120度回転します。
• 次に、手順B(=L')によってNB'にあったPNB'がNへ移動します。PNA'(=PN)がNから一旦追い出されます。
• その次に手順A'(=(U R U' R')x2)を行うと、PNB'がその場で時計回りに120度回転します。
• 最後に手順B'(=L)を行うと、PNB'がNB'へ戻ります。同時に、追い出されていたPNA'(=PN)がNへ戻ります。

よって、このCommutatorでは2コーナー(UBL,ULF)の回転のみが起こります。
手順AでPN(UBL)が移動しないため(N=NA')です。

他の例を見てみましょう。

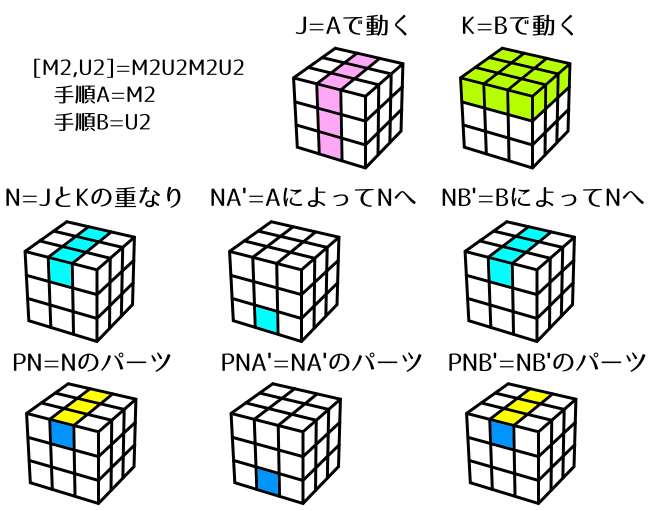
[M2,U2] = M2 U2 M2 U2
2x2交換を行うパターンです。
NにはUFとUBが含まれます。手順BはNにおいて(UF⇔UB)の2点交換を行うため、Nにパーツの出入りがありません。よって、(N=NB')です。手順Aと手順A'によってBによる2点交換の対象となるパーツがそっくり入れ替わるため、(UF⇔UB)(DF⇔DB)の2x2交換が行われます。

[R U R' F R' F' R,E] = R U R' F R' F' R E R' F R F' R U' R'
2エッジ反転手順です。(N=NA')
手順AでE列を崩さずにエッジ(RF)を反転し、手順Bで反転されるエッジを入れ替えています。

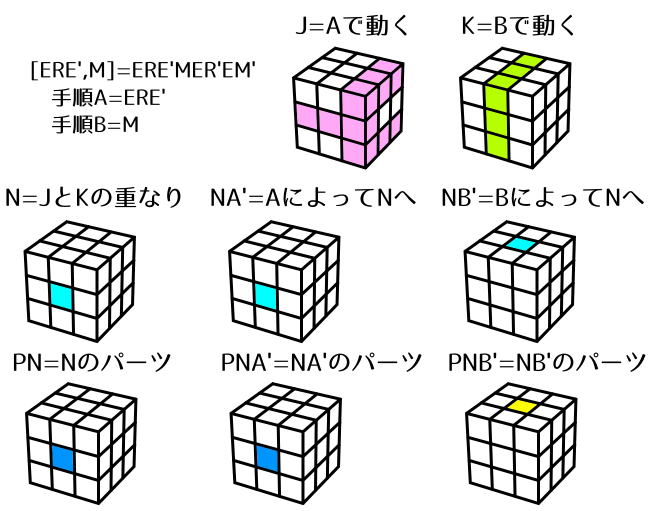
[E R E',M] = E R E' M E R' E M'
2センター回転手順です。(N=NA')
手順AでM列を崩さずにF面センターを時計回りに90度回転させ、手順Bで回転を受けるセンターを入れ替えています。U面センターは反時計回りに90度回転します。

時々使われるコミュテーター(2)

N=NA'とN=NB'のどちらか一方だけが成立していて、NA'とNB'が重なるCommutatorです。
よく見るのは[M',U2]のようなタイプです。(というかこれしか見ない)

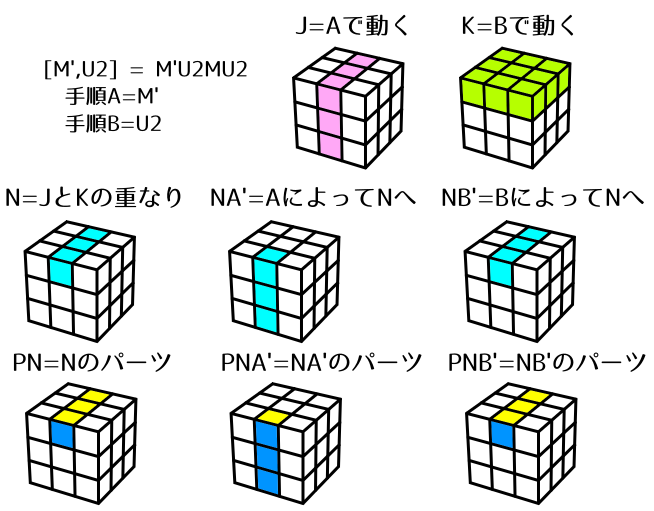
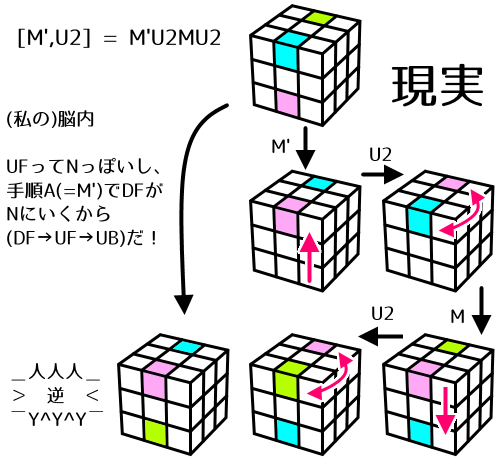
[M',U2] = M' U2 M U2 (N=NB')

• 手順A(=M')によってPNA'がNに入ります。
• 手順B(=U2)によってPNA'はNから移動せず、その場で2点交換(UF⇔UB)を行います。
  ただし事前にM'を行っているので、実質的には(DF⇔UF)です。
• 次に手順A'(＝M)を行うと、PNA'が元の位置に戻ります。
• 最後に手順B(=U2)を行うと、2点交換(UF⇔UB)が行われます。

よって、このCommutatorでは2点交換が2回行われます。
ただし一部が重なっており、パーツの移動は(DF⇔UF)→(UF⇔UB)となるため、
結果として3点交換(UF→DF→UB)が行われます。

複雑なコミュテーター

正直これをしっかり理解しても役に立たないと思います。
それでもいいよって人だけ読んでください。

まず、新しく領域を定義します。

• HB = Nのうち手順BでNから出ていく領域 = (NB-N)B'
• HA = Nのうち手順AでNから出ていく領域 = (NA-N)A'
• HA' = Nのうち手順A'でNから出ていく領域 = (NA'-N)A
  補足

  「(ほにゃらら)A 」は、「領域ほにゃららに手順Aを行ったときの移動先」の意味です。
  「(ほにゃらら-ふにゃらら)」は、「領域ほにゃららから領域ふにゃららを引いた領域(差集合)」の意味です。
  よって、例えば(NB-N)B'は、
  「領域Nに手順Bを行ったときの移動先から領域Nを引いて、それに対し手順B'を行ったときの移動先」
  という意味になります。ややこしいにも程がある

  次に、新しくパーツを定義します。
• PA = (HB)A'に入っているパーツ。Commutatorによって(PA)Aへ移動する。
• PB = ((HA')B'-N)に入っているパーツ。Commutatorによって(PB)BA'へ移動する。
• PN = HAに入っているパーツ。Commutatorによって(PA)B'へ移動する。

では、例を見てみましょう

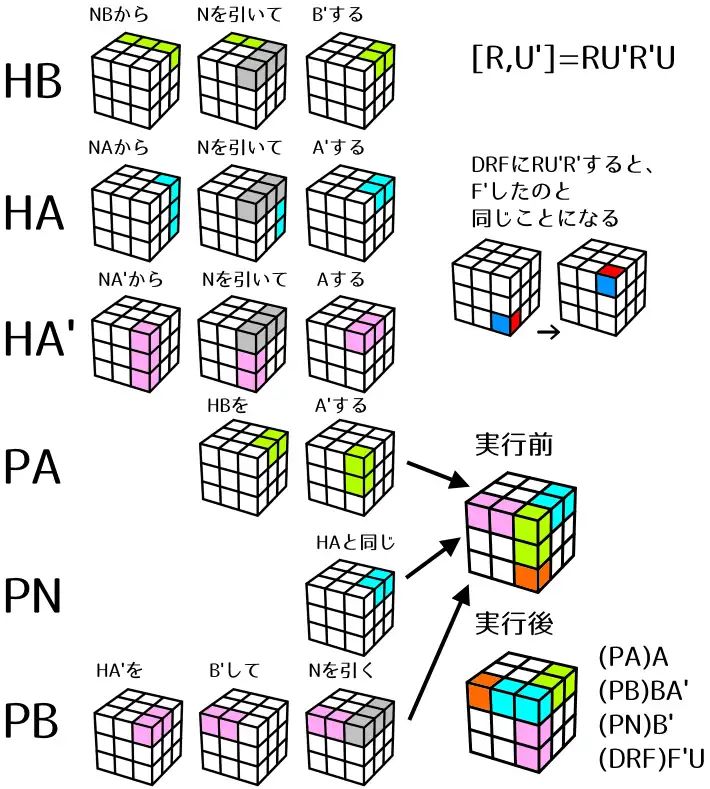
[R,U'] = R U' R' U

• HB = UR,URB なので、PA = FR,UFR です。UR,URB へ移動します。
• HA = UR,URB なので、PN = UR,URB です。UF,UFR へ移動します。
• HA' = UR,UFR なので、PB = UF,ULF です。FR,FDR へ移動します。

PA,PB,PNは3サイクルのように動きますが、元の場所にぴったり収まるわけではありません。
今回はDRFが居場所を追い出されています。
DRFは全ての手順の影響をうけます。R U' R' はDRFに関してF'に等しいため、DRFはF' Uと移動する、と言い換えることもできます。

このように、ABA'B'のすべてに影響を受けるパーツをPQと名付けます。
PQ = (HA'-HB)A' です。*5
似たようなものに ABA' もしくは BA'B' の影響を受けるパーツがあり、これををPCと名付けます。
PC = (J+K)-(HA+(HB)A'+(HA')B+PQ) です。*6
複雑なコミュテーターではPQ,PCが出現します。

PCが出現する例を見てみましょう。

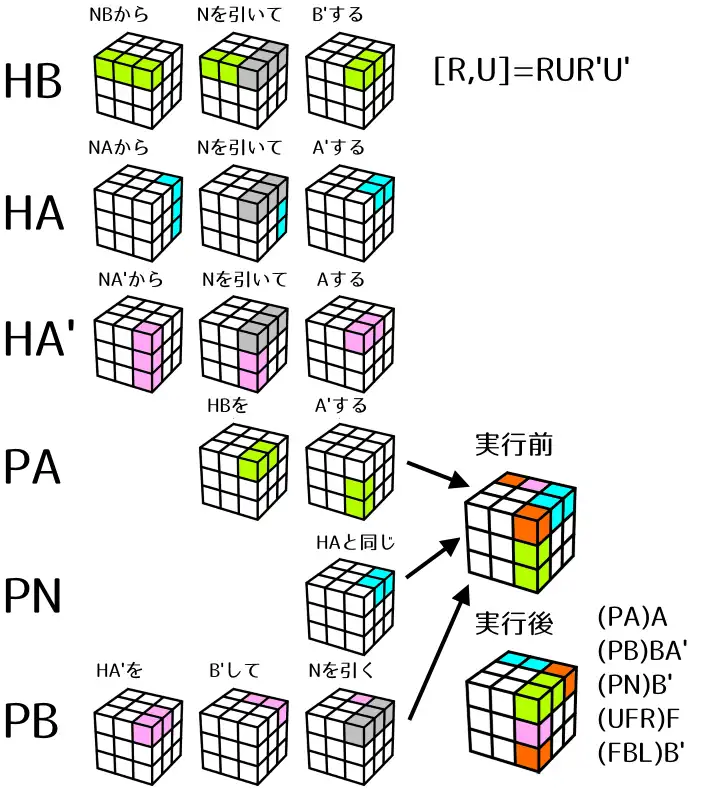
[R,U] = R U R' U'

• HB = UR,UFR なので、PA = FR,DRF です。UR,UFR へ移動します。
• HA = UR,URB なので、PN = UR,URB です。UB,UBL へ移動します。
• HA' = UR,UFR なので、PB = UB です。FR へ移動します。

PQはありません。
PCは2つあります。

• FRUはABA'(=RUR':実質F)の影響を受け、FDRへ移動します。
• UBLはBA'B'(=UR'U':実質B')の影響を受け、RBUへ移動します。

PQとPCが同時に出てくるパターンもあります(例:[RU',F])。今回は省略します。

何もしないコミュテーター

JとKが重ならない場合、Nが存在しません。
よってNA'とNB'も存在せず、Commutatorはパーツを一切変化させません。(例：A = R, B = L)
このとき必ずAB = BA となります。

• ABA'B'=変化なし
• ABA'B'(BA)=BA　……末尾にBAを追加
• ABA'(A)=BA　　　 ……B'Bはパズルを変化させないので消去
• AB=BA　　　　　　　……A'Aはパズルを変化させないので消去

終わりに

今回の内容だけではCommutatorを使えるようにはなりません。なったらすごい。他にもたくさんの知恵が必要です。それらはネット上にタダで転がっていますので*7、ぜひそれらも見てみてください。色々理屈を述べてきましたが、Commutatorを使いこなせるかどうかは結局のところ個人の努力による所が大きいと思います。何かを学んだら、とにかくいろいろ試してみましょう。試行錯誤を重ねて、よいCommutator使いになってください。
ここまでお読みいただきありがとうございました。


Tag: 知識・理論