*Definition [#ia7890ac]
A Tychonoff space is called realcompact if every ultrafilter of [[zero set]]s with [[cip]] is [[fixed]].

*Property [#w8b6a596]
-A space is realcompact if and only if it is homeomorphic to a closed subspace of a product of real lines.
-Every Tychonoff Lindeloef space is realcompact.
-If X is a Tychonoff space, the following conditions are equivalent:
++X is realcompact;
++X is the intersection of all [[cozero set]]s in the Stone-Cech compactification of X;
++X is the intersection of all [[σ-compact]] subspaces of the Stone-Cech compactification of X;
++every [[maximal]] cozero cover has a countable subcover;
++if A is a [[stable family]] of closed subsets in X with [[fip]], A has a nonempty intersection.
-The image under a [[perfect]] mapping of a normal realcompact space is also a realcompact space.
-Realcompact implies both [[almost realcompact]] and [[almost* realcompact]].
-X is realcompact iff for each point p in βX-X, there exists a continuous function f on βX such that f(p)=0 and f is positive on X (where βX denotes the Stone-Cech compactification).
-If C_ρ(X) represents the collection of continuous functions with realcompact support, then X is realcompact iff C_ρ(X) = C(X).
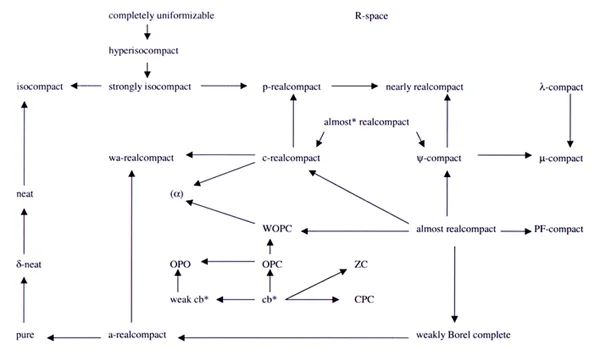
-See the following figure for implication between the related properties.
&attachref(./realcom1.jpg,nolink);
*Reference [#p62d19a3]
-Zdenek Frolik, ''A generalization of realcompact spaces'', Czechoslovak Mathematical Journal, Vol.13 (1963), No. 1, 127-138.
-John J. Schommer and Mary Anne Swardson, ''Almost realcompactness'', Commentationes Mathematicae Universitatis Carolinae, Vol.2 (2001), No.2, 383-392.
-Nancy Dykes, ''Generalizations of Realcompact Spaces'', Pacific Journal of Mathematics Vol. 33, No.3, 1970.
-K.P.Hart, J. Nagata and J.E. Vaughan, ''Encyclopedia of general topology'', Elsevier Science.
-M. Mandelker, ''Supports of continuous functions'', Trans, Amer. Math. Soc, 156 (1971), 73-83.
-http://www.utm.edu/staff/jschomme/realcom.html