前回の課題の講評
学内限定
http://www.ugs.kochi-tech.ac.jp/kutpg/internal/contest/algorithm_workshop2/
探索とは
探索とは、問題の解を、入力で与えられた情報から探し、適切なものを見つけ出す手法です。
配列の中から、特定の値を探す線形探索や二分探索も探索の1つです。
探索の手法は多数ありますが、今回は木探索の手法の1つ、深さ優先探索を扱います。
深さ優先探索では、解を探す際、考え得る組み合わせからすべてを試し、最も適切なものを解とします。*1
すべての可能性を試す必要があるため、計算量は一般的に大きく、大きな入力に対しては実行に時間がかかります。
その場合は、別のアルゴリズムを使う必要がありますが、小さな入力が保証されている場合、深さ優先探索は十分に使えるアルゴリズムです。
深さ優先探索について
深さ優先探索は、英語では Depth-First Search となるため、DFS と略されます。
以降、深さ優先探索のことは、DFS と記します。
DFS では、得られる可能性をすべて試し、解を探します。
一般的に、DFS をプログラムで実装する場合は再帰関数となります。
再帰関数では、初期状態と終了条件が必要です。
初期状態は、再帰関数を呼び出す時に引数として与え、終了条件は再帰関数の内部で条件分岐によって判定します。*2
例えば、家から学校までの経路を探索したいとします。
その場合の初期状態は「家」で、終了条件は「学校」です。
これを、木 *3 で表す場合、次のように表されます。
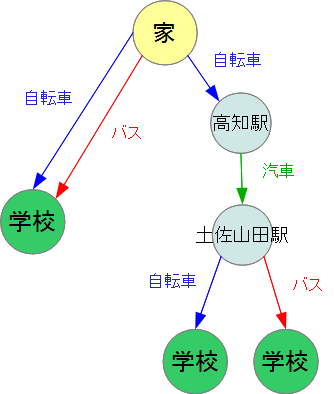
木の根 (ルート) が初期状態で、葉が終了条件に相当します。
これを、再帰関数で探索した場合、状態遷移が次のように発生します。
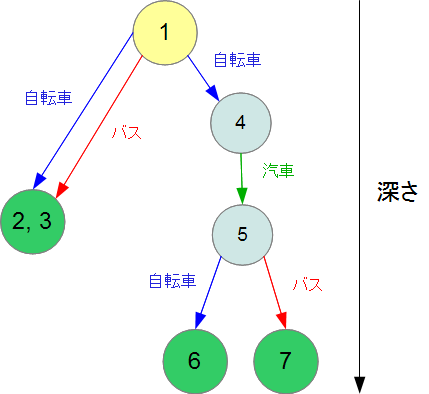
進めるだけ深く進み、それ以上進めなくなったら戻るという動作をしていることが分かると思います。
このような動作をするため、深さ優先探索と呼ばれるのです。 *4
グラフの連結判定
深さ優先探索の例として、無向グラフが連結グラフ *5 かどうか判定するプログラムを考えてみたいと思います。
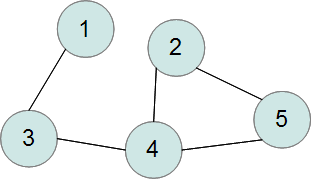
グラフが連結であれば、ある1つの頂点から出発して、すべての頂点へ到達することができるはずです。
これを利用して、C言語を使い DFS でグラフの連結判定をしてみましょう。
連結判定を行う際の変数として、頂点に到達したかどうかを保持する変数 flag を作成しておきます。
また、グラフの辺を保持する変数 edge も作成しておきます。
#define
int flag[N]; // 頂点に到達したかどうか
int edge[N][N]; // 辺の情報再帰関数を呼び出す前に、変数 flag には初期値として、到達していないことを表す 0 を代入しておきます。
グラフが連結であれば、どの頂点からでもすべての頂点に到達できるため、初期状態はどの位置でも構いません。
辺を表す変数 edge は、edge[a][b] で a から b への辺を表し、もし辺が存在するなら 1、存在しないなら 0 が代入されているとします。
DFS によって頂点に到達できるか調べたら、すべての頂点したかどうかを変数 flag をみて判定します。
// 解を求める関数
void solve(void){
int i;
// 初期化
for(i = 0; i < N; ++i){
flag[i] = 0;
}
// DFS (初期状態: 頂点 0)
dfs(0);
// すべての頂点に到達したか調べる
for(i = 0; i < N; ++i){
if(!flag[i]){ // 到達していない頂点を見つけた
break;
}
}
if(i == N){
printf("グラフは連結です。\n");
}
else {
printf("グラフは連結ではありません。\n");
}
}再帰関数 dfs では、現在の頂点から行くことが可能である頂点へ行くといった動作をします。
既に到達した頂点へは、再度行かないように変数 flag を使います。*6
// 深さ優先探索
void dfs(int vertex){
int i;
// 既に到達済みの場合
if(flag[vertex]) return;
// 到達済みとして保存
flag[vertex] = 1;
// 頂点 vertex と辺がある頂点へ訪問
for(i = 0; i < N; ++i){
if(edge[vertex][i]){ // 頂点 vertex から i へ辺がある
dfs(i); // 頂点 i へ移動
}
}
}課題
KOJ にある問題を解いてください。
使用する言語は、プログラミング言語であれば自由です。
問題 URL
http://kut-oj.appspot.com/contest/algorithm_workshop3/
- 問題増やしました! (2012/6/15, 16)
解説, 講評 (学内限定)
http://www.ugs.kochi-tech.ac.jp/kutpg/internal/contest/algorithm_workshop3/
挑戦課題
すべて、深さ優先探索 (DFS) の問題です。*7
ミス等あれば、編集するかコメントをいただけたら嬉しいです。
