すなわち受験数学。*1
1000以下の素数は250個以下であることを示せ。(一橋大, 2021)
「良問」として紹介されていたのを偶然見かけた。
(当時話題になった問題らしい)
でもこれ大学入試に出す課題としてはあんまり良問じゃない気がする。
- 一橋大
- 街道のすぐ脇に脈絡なく設置された固定シンボルのボスモンスターみたいな存在。体制として文学と縁無さげだし私はよく知らん。
プリ証明
- プリ
- preparing 仕込みの意。
区間[1,1000]において素数ではない整数が(1000-250)=750個以上示されるならば、題意が満たされる。
- ①明らかに600個ほど視えている素数ではない数(2の倍数、5の倍数)について考える。
- ただし2,5は素数であるから除外し、素数ではない数が598個示された。
1 2 3 4 5 6 7 8 9 10 ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ 991 1000
- ②3の倍数について考える。
- 3×1から3×333までの333個について、
(a) 2の倍数は①と重複するため除外する。
(3×2,3×4,…,3×332、計166個)
(b) 5の倍数は①と重複するため除外する。
(3×5,3×10,…,3×330、計66個)
(c) 素数である3自身は除外する。
(a),(b)両操作において2かつ5の倍数=10の倍数33個を二重に除外してしまったため、再び加算する。
333-(166+66+1)+33=133
少なめに数えて、*2素数ではない数が新規に130個示された。
- ③その他の素数×その他の素数について考える。
- 区間[1,(当該の数-1)]から自明に得られる7つの素数、7,11,13,17,19,23,29の二項乗算について考える。
29×29<1000であるため、異なる値の組み合わせから7C2=21種類、自乗から7種類の値を得られる。
ゆえに、素数ではない数が新規に28個示された。
このとき(598+130+28) = 756であるから、区間[1,1000]において、少なくとも756個の整数が素数ではないと示された。
よって、題意は示された。//
コネ解題
- コネ
- connected 関連の意。
「あなたエラトステネスのふるい覚えてましたか？」が初手にして最大のハードル。
すなわち「素数の話を初めて聞いた小学生なり中学一年生なりのあなたは、それを『面白い！』と思える生徒でしたか？」の言い換えであろう。
- あんまり良問じゃない
- だってこれ算数だし。
この問題に対してむずかしそうな数学的概念を持ち出す解説(検索したらいっぱいでてきた)はみな的を外している。- 前セクションの解答例も、(①でエラトステネスのふるい使うのであれば)本当は②でベン図、③で総当り表なり樹形図なりを記す方が理にかなう。
- 「短い制限時間で発想力を問う課題」はストレス耐性に依り過ぎる
- エラトステネスのふるいそれ自体は素朴なアイデアであるから、知らないor忘れていた人であっても比較的再発明しやすい。
一橋大学受ける層なら、2日ほど牢屋に閉じ込めて頭ひねらせればみな思い付くはずだ。
しかしこの「しやすい」は自然体を前提としている。
「直近の人生賭けて試験会場に座る高校生その他がプレッシャー下で思い付くか？」となると、数学的センス如何よりむしろストレス耐性テストではないか。 - 「そのまんま数えるアプローチ」の所在
- 「数えて済むなら抽象化しない方が早いこともある」なる身も蓋もないが有用な算術ツールは、しかし特定の環境以外で接する機会が乏しい。
特定の環境とは何か。中学受験。
中学受験的アプローチを国立大学の入試が要求する／国立大学の入試問題が中学受験勢をソフトに優遇するとき、人文科学の側ではハビトゥスとか文化資本とか蠢き始める。平等であるが公平ではない。- 問われているのはホンマに柔軟な発想力か？
- より説得力を生みそうな論点
- 私が見た瞬間解き方分かってしまう問題は大学入試数学の問題として不適だろう。もっと加法定理とかのよく分からんやつらで弾け。sinプリcosブルcosプリsinブル。
- 加法定理とかのよく分からんやつらで弾け。
- 東大(1999)「弾いたぞ」
四半世紀先回りされていた。東京大学に250プリポイント進呈。
円周率が3.05より大きいことを証明せよ。(東京大, 2003)
腐るほど引用されるやつ。
たぶんここから始まった流行なのだろう。
(「抽象化は手段の一つであり作法ではない」と理解しているか？を問うシリーズ)
- ただし、この問いは解き方が即座に分かっても[どう円周率が絞り込まれたか歴史として知っていても]実計算なくしては正答へ辿り着けない。ゆえ私は入り口までしか解けない。
→真に総合的な数学力を問うている設問。💮
- 私は入り口までしか解けない。
- 3.05指定が数学としての実計算コストを高めている。
具体的には余弦定理の呪文とかその辺きれいに忘れたため、正十二角形×余弦定理で足りるかどうかも確かめられない。
てっぺん15°の三角形とかどうすればいいかみごとにわすれた。- 「3より大きいことを証明せよ」なら小学生でも通せる。
- 私はこのくらいのクイズの方が安心できてすき。あなたはどうですか。
- 「3より大きいことを証明せよ」なら小学生でも通せる。
てっぺん15°の三角形とかどうすればいいかみごとにわすれた。
加法定理。(45-30とか60-45とか)
→余弦定理。
- どのみち綺麗な数字は出てこない。
なにこのページ
「受験産業や教育ビジネスは、文化資本なる概念の現代日本における表出面でありうる」と書いたら人文科学の話に落ちた。
ぷり。
- ぷり
- principal(主要)の意。
余弦定理。
law of cosinesらしい。コサイン法則とか呼んでくれたら少なくともコサイン使うのは絶対忘れないのにね。余弦って言われても分からなくない？
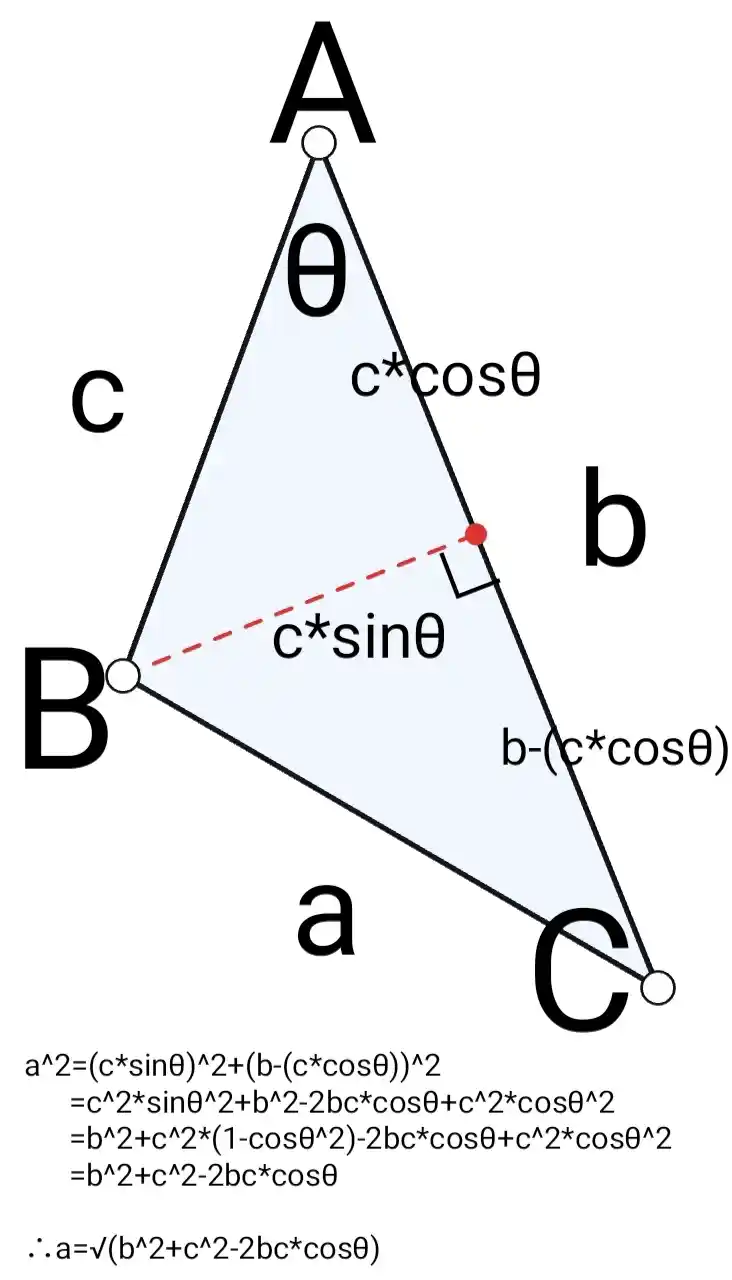
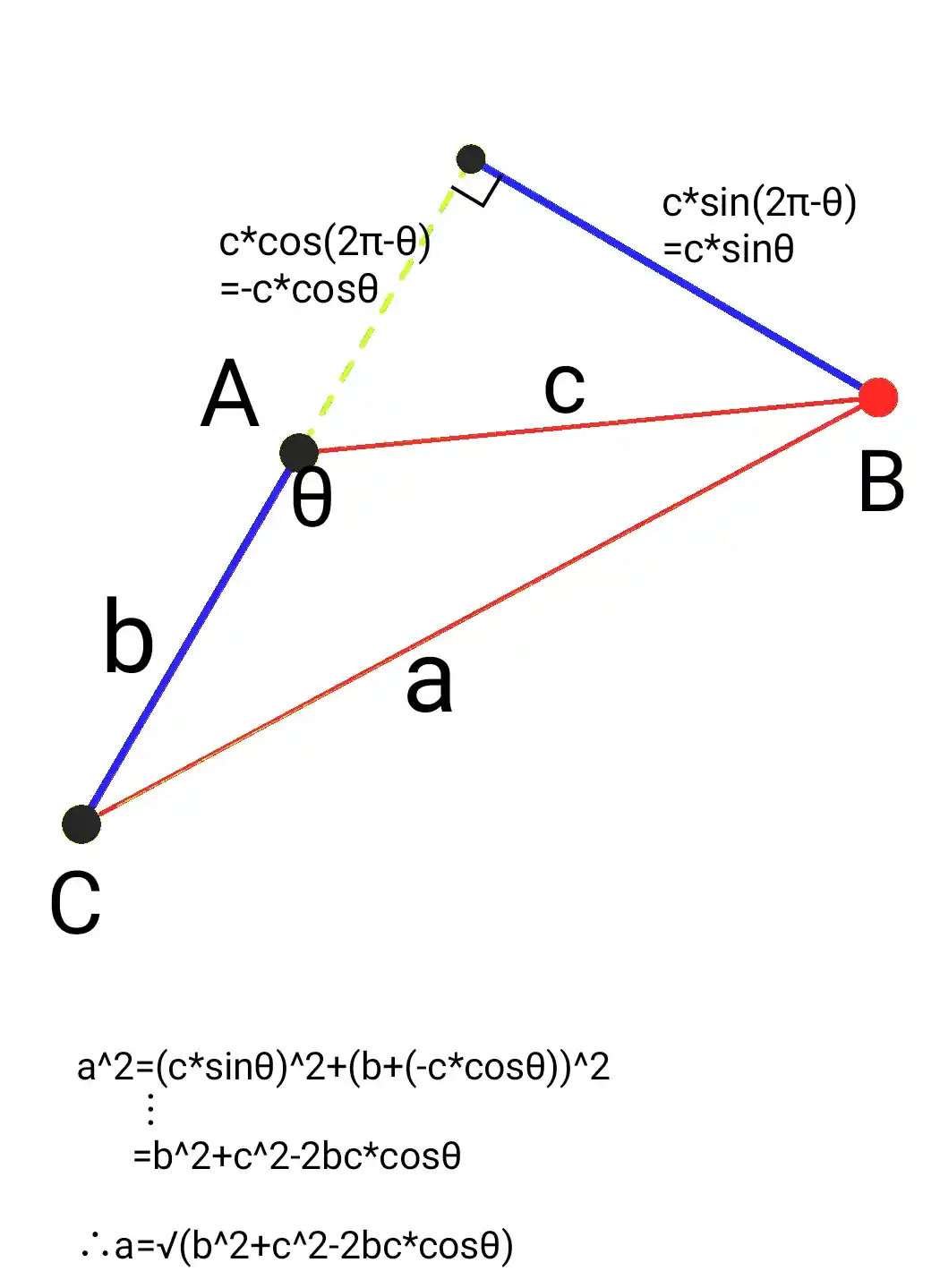
こっちは思い出せた(一般化された三平方の定理)。三角関数二乗するときってcos^2(θ)みたいな書き方するんだっけ？まあ消えるしいいか*3。
- (サインθの2乗)+(コサインθの2乗)=1
- サイン・コサインの定義…から単位円内に導かれる三角形…に対しての三平方の定理
これも思い出せた。
加法定理。
ぷり。
(こいつは結論ありきで仕掛けないとまず辿り着けそうにないような手順で導かれていた。だから詰まりポイントなのだろう。見つけたやつはえらい。)
三角関数(人文科学)
正弦定理。
接弦定理
仲間みたいな顔で並ぶな。
弦
つる。
ベクトルの内積
私(高校時代)の疑問︰こいつ習う科目って物理の方が適切じゃない？
- 定義①
- 成分ごとに掛け合わせて合算した数値。
- 定義②
- (ベクトルAの長さ)×(コサイン用いてベクトルAに影落としたベクトルBの長さ)で出る数値。
- なんか同じもんが出てくるんだって。すごい。
- 理屈
- ぷり。
- なんか同じもんが出てくるんだって。すごい。
- 実用
- 2つのベクトル間の関係(向きのズレとか)を計る際に用いられるようだ。もっと具体的にはゲームとかCGとかで相対的な方向や角度計ったり物理演算に使ったりするらしい。やっぱきみ物理の子じゃない？
- 実用ありきの概念なのになんか純粋数学っぽく教わるからよく分からないのかもしれない。
ベクトルの外積
ぷり。
- 三次元空間前提(立体方向に直交するベクトル？)らしい。フレミングの左手の法則みたいな図が描いてあった。わかりゃん。
高校数学の範囲では触れないようだ。つまり私は一度も触れていない。触れないという話だけ聞かされて頭に残っていたのかもしれない。
- 触れないようだ
- しかし受験数学的には(カリキュラム外で)公然と実用されるらしい。じゃあ触れてるかもしれない。知らん。
- どのみち私の頭の中には名前しか残っていない。