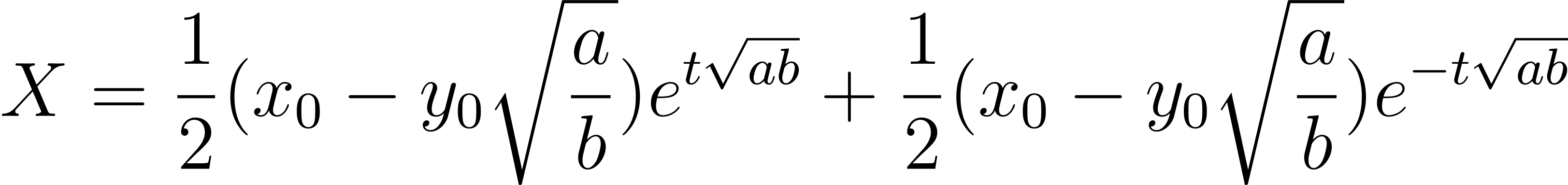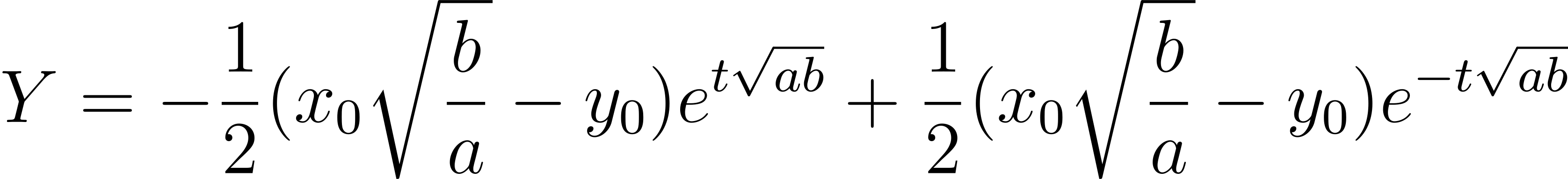新規
編集
添付…というコトで、先までの記述は ある程度 事実に即した描写である
ただ、言及されている範囲でも “ 直感的に ” 矛盾を感じる人が おられるかも知れない
まず戦力は数と質に分割でき、執筆者当人も その点については間接的に
> それぞれの人員に質的な違いは無いものとして、( 後略 )
と触れており、現実には人数差や練度、装備の良悪に差があって、戦力を構成する要素との認識が伺える
そうなると例えば勢力同士や勢力内のユニット割合などに “ 戦力 ” のバラツキがある場合、｢ 各戦力の 安重根 
平方根となると、どういう内訳になるのだろう ? ｣ などといった疑問はワリと自然とも思われる
時に数学や科学の知見を利用して統計的な命題に取り組む分野としては統計学がワリと有名だろう
ちなみに、世間では混乱があるとも聞くが統計学とは純粋な数学の分野ではなく数学を重用する応用科学の類いである
つまり実学として有意義な手法の開発や定理の探求に対するウエイトが比較的大きく、無関心でないにせよ原理、理論の探究、解明には消極的である
そんなワケで、同じく実学を重視する工学などと同様、統計学も定型的なノウハウを多用する慣習が幾つか知られており、特に有名なのが数理モデルという概念を やたらめったら 頻繁に用いた対象の説明である
例えば本稿の場合、統計学風なり統計学調に解法を求める場合は 二項 ベルヌーイ分布*1と指数分布という確率分布の合成によるモデリングが教科書的であるという
つまり 2 つの事象に分けて表現したあとで一方の関数に残り一方の関数を変数と見なして代入するワケである
amount_of_variant
この場合、
( 戦闘開始後の経過 ) 時間
→ t
自分の戦力 ( の初期値 )
→ x₀
自分の戦力の強さ
→ a
相手の戦力 ( の初期値 )
→ y₀
相手の戦力の強さ
→ b
という 5 項目を変数とし、以下 2 つの結果が得られるような方程式に落とし込むコトになる
自分の残戦力
→ X
相手の残戦力
→ Y
two_Pattern_events
まず 二項 ベルヌーイ分布というのは、一定確率で起こる 2 パターンの出来事が次に再び起こった時にどっちに転ぶかを数式化したものである
本稿の場合、欲しい統計量は特定の兵士に攻撃が向かった場合の死亡確率になろうから、横軸が戦いの起こった回数、縦軸が攻撃を被ったコトによる死亡確率を取る確率密度関数のグラフをイメージしてもらえば良いだろう
次に指数分布というのは、ある確率で起こるコトが次に再び起こるまでの時間と確率の関係を数式化したものである
ただし本 稿 項の場合、“ 一定確率で起こるコト ” が次に再び “ 1 回こっきり ” 起こるまでの時間を数式化したいワケではなく兵士が絶命する累積数が “ 起こるコト ” として欲しい統計量であろうから、横軸に時間、縦軸に残兵数または累積死者数を取る累積分布関数のグラフをイメージしてもらえば良いだろう
すると、
- 兵士の絶命イベント発生タイミング
♪ - 交戦による死亡確率
という 2 つの統計量を示すグラフが描けるハズだ
前者だけだと交戦の結果として生きているのか死んでいるのか分からず、後者だけだと いつ ( のタイミング ) まで生きているのか分からんので、2 つの方程式を合成させるコトにより ｢ 交戦が行われ、その結果、生きていたり死んでいたりする ｣ 様子を数式化するワケである
すると、以下のような連立方程式が成立するらしい
なお、グラフ化すると こんな感じ
