編集時Ver3.1.2.4
Bread Boardの基礎的な部分の補足です。
1.ブレッドボードができること
ACBが 情報入力→機器に出力 をするブロックだとすると、
ブレッドボードは 情報入力→計算→命令を出力 ができるブロック。
例えばビークルの高度を取得し、低ければ船首を上げ、高ければ船首を下げることなどができる。
数値の扱いにとても長けていて、ややこしい条件分岐などもこなす。
複数のACBの機能をひとまとめに代替することもできるので便利。
2.ブレッドボードにできないこと
出力が貧弱で、ACBのように機器を直接動かすことはできず、ドライブ値しか出力できない。
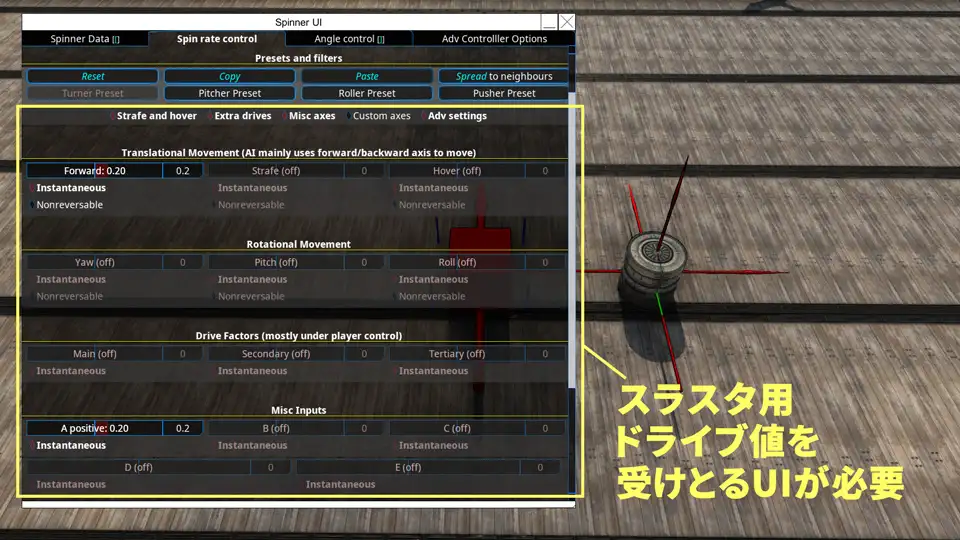
このため、スピンブロックやジェットなどのようにスラスタ用のドライブ値を受け取ることができるブロックしか操作できないことに注意する。*1
入力情報はかなり豊富に取れる。
AIの目指しているヨー・ピッチ・ロールが取得できないので、原則AIPIDの代替はできない。
3.各部名称
四角いものがコンポーネント。*2
これらをリンク*3で左から右に情報をつないで渡していく。
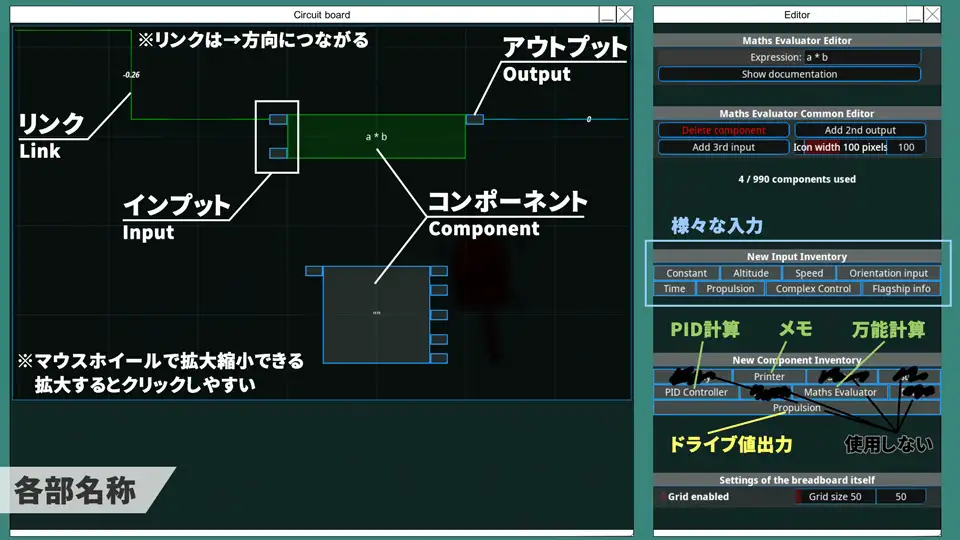
Maths Evaluatorが万能なのでMultiply・Switch・Sum・Clampは無理して使わなくてもよい。
PropulsionはDrivesの機能も持っている。
4.操作方法
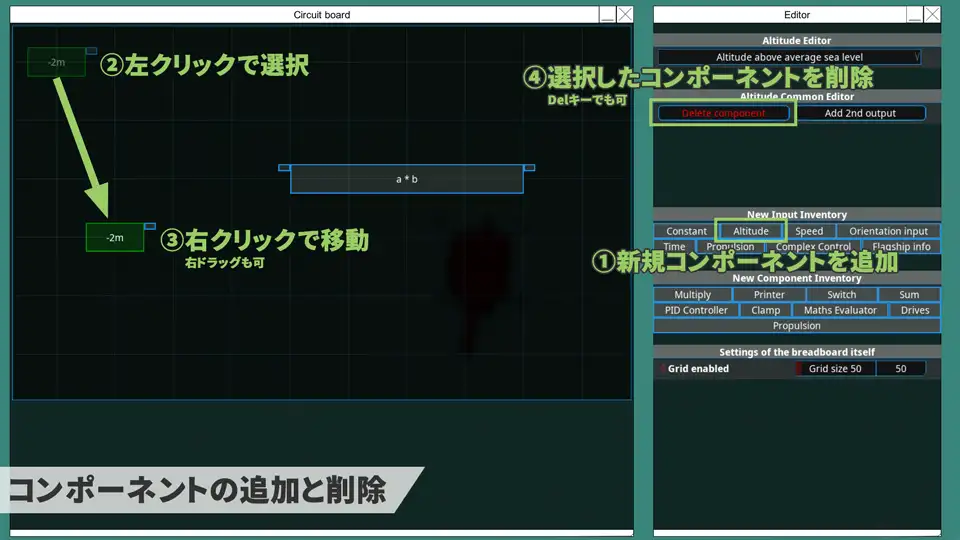
- 右のボタンをクリックで新規コンポーネントが左上に出現する。
- コンポーネントを左クリックで選択し、
- 右クリックで指定した位置に移動する。
- 右上のボタンをクリックで削除できる(Delキーでも可)。
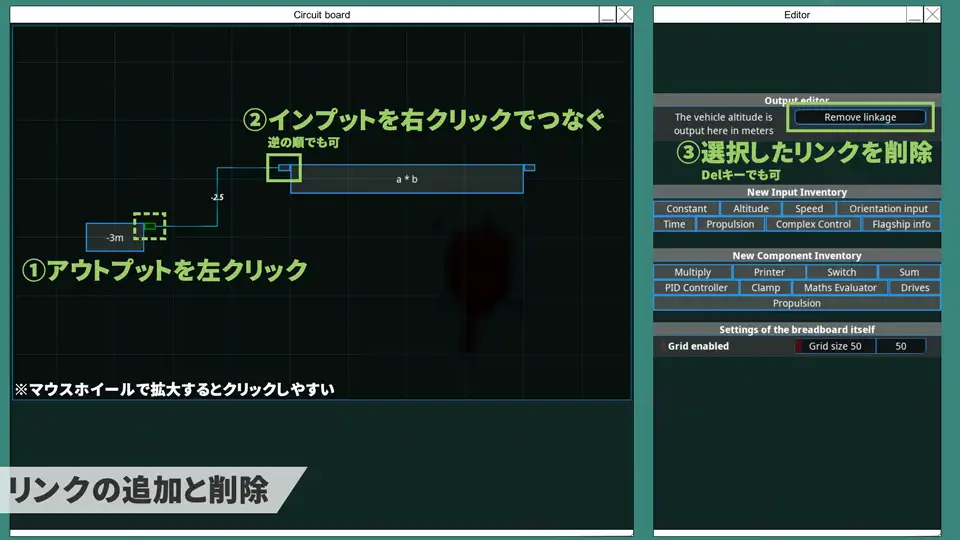
- コンポーネントの右上のアウトプットを選択し、
- 他のコンポーネントの左上のインプットをクリックでリンクをつなぐ。
- 右上のボタンをクリックで削除できる(Delキーでも可)。
5.Maths Evaluatorの使い方
足し算、かけ算からベクトル解析までこなす最強のコンポーネント。
計算式一覧
| Logic Gate | 名称 | 論理ゲート |
| 説明 | NOTやORなどの論理回路になるブロック。入力の解釈には3種類あり、上から ①0以外 ②0より大きい ③1以上 | |
| NOT | 説明 | 論理否定。出力を反転する |
| AND | 説明 | 論理積。入力ノード両方に入力があった時に出力する |
| OR | 説明 | 論理和。入力ノード1か所以上に入力があった時に出力する |
| XOR | 説明 | 排他的論理和。入力ノードのどちらかに入力があった時のみ出力する |
| NAND | 説明 | 否定論理積。入力ノード両方に入力がない時に出力する |
| NOR | 説明 | 否定論理和。入力ノードに全く入力がない時に出力する |
| XNOR | 説明 | 否定排他的論理和。入力ノード両方の状態が一致している時に出力する |
| Max/Min | 名称 | 最大/最小 |
| 説明 | 複数の入力に対してそのうち最大もしくは最小の値のみを出力する。第一出力末端がその値、第二出力末端が何番目の入力を出力しているかを出力する | |
| Sorter | 名称 | 並び替え |
| 説明 | 複数の入力に対して値の小さい順もしくは大きい順に出力の順番を調整する | |
| Comment | 名称 | コメント |
| 説明 | **加筆求む!** | |
| Accumulator(with threshold) | 名称 | 累算器(閾値付き) |
| 説明 | **加筆求む!** | |
| Threshold | 名称 | 閾値 |
| 説明 | **加筆求む!** | |
| One shot | 名称 | ワンショット |
| 説明 | **加筆求む!** | |
| Delay Pulse | 名称 | 遅延パルス |
| 説明 | coming soon... | |
| Playback | 名称 | 音声再生 |
| 説明 | 音声ファイルを再生するコンポーネント。デフォルトで入っているMihoの音声のほか、C:\Users\[ユーザー名]\Documents\From The Depths\Sounds内に入れたファイルを認識する。0以上の数値が入力されたときに再生される | |
| ① | 説明 | 誰の音声を再生するかプルダウンから選択できる |
| ② | 説明 | 音声ファイルがまとめられているときはここから選択可能 |
| ③ | 説明 | 「#+ファイル名」で再生する音声ファイルを指定できる |
| Delay | 説明 | 入力ノードに数値が来てからどの程度遅れて再生するか設定できる。上限と下限を0~10秒の間で設定可能 |
| Audible distance | 説明 | どの範囲まで音が聞こえるか設定できる。上限と下限を1~5000mの間で設定可能 |
| Pitch | 説明 | 再生時の音声のピッチを設定できる。上限と下限を0.1~10の間で設定できる ※音程と一緒に再生速度も変わる |
| Doppler | 説明 | 音声のドップラー効果の強さを設定できる。上限と下限を0~1の間で設定できる |
| Generic block setter | 名称 | 汎用ブロック設定 |
| 説明 | 数値を設定できるアイテムに対してBBから値を設定できる。ブロックのアイテム名の後ろにある(#○)はいくつのアイテムを設定しようとしているかの数 | |
| Block name filter | 説明 | そのブロックについている名前(shift+Nで付けられる奴)でフィルターを設定できる ※名前については"完全一致"ではなく"含む"なので命名時注意! |
| 項目② | 説明 | 設定したいアイテム |
| 項目③ | 説明 | そのアイテムのどの値を設定するか |
| Maths Evaluator | 名称 | 演算評価 |
| 説明 | 最強の演算装置。第一入力末端から第五入力末端までの入力をExpession内に記述された式で演算し、その値を出力する。出力末端は最大で5つで、式が1個ならすべて同じ値を出力する 追記:ver3.9.0.0より入力末端と出力末端の個数はアルファベットと同じ26個に増加しました | |
| Expression | 説明 | ここに記述された式の演算を行う 例:a=3 b=10 c=1の時、(a*b)/c → 出力値30 複数の式をまとめる時、(a*b)/c,a+b+c → 第一出力末端の出力値30、第二出力末端の出力値14 v3.9.1.0より改行ができるようになりました |
| Icon width | 説明 | ノードの幅を5~200ピクセルの間で設定する |
| Show documentation | 説明 | ここに各演算子や入力変数名、関数などの説明がある内容については以下の通りである |
| Constants/Inputs 以下定数と入力値(オペランド) | ||
|---|---|---|
| Pi | 説明 | 円周率(3.14159265358979) |
| Right | 説明 | x方向のベクトル成分(1をセット) 例:Right*10→(10.0 0.0 0.0) |
| Up | 説明 | y方向のベクトル成分(1をセット) 例:Right*10→(0.0 10.0 0.0) |
| Forward | 説明 | z方向のベクトル成分(1をセット) 例:Right*10→(0.0 10.0 0.0) |
| a | 説明 | 第1入力末端入力値 |
| b | 説明 | 第2入力末端入力値 |
| c | 説明 | 第3入力末端入力値 |
| ︙ | ︙ | ︙ |
| z | 説明 | 第26入力末端入力値 |
| Functions 関数(※一部順不同) | ||
| (戻り値の型) (関数の形) | 訳文 | ※戻り値の型についてはnumber(数値)とvector(ベクトル)の要素はdouble型(v3.9.0.0~)、integer(整数)はlong型です |
| number Sin(number x) | 訳文 | xの正弦を数値で返します。xは度数で認識されます 例:Sin(30)→0.5, Sin(-30)→-0.5 |
| number Cos(number x) | 訳文 | xの余弦を数値で返します。xは度数で認識されます 例:Cos(60)→0.5, Cos(240)→-0.5 |
| number Tan(number x) | 訳文 | xの正接を数値で返します。xは度数で認識されます 例:Tan(45)→1 |
| number Sqrt(number x) | 訳文 | xの平方根を数値で返します 例:Sqrt(625)→25 |
| number Asin(number x) | 訳文 | xの逆正弦を度数で返します 例:Asin(1)→90 |
| number Acos(number x) | 訳文 | xの逆余弦を度数で返します 例:Acos(-1)→180 |
| number Atan(number x) | 訳文 | xの逆正接を度数で返します 例:Atan(1)→45 |
| number Atan2(number y, number x) | 訳文 | 点(x, y)に対応する角度を度数で返します 例:Atan2(√3/2, 1/2)→60 |
| number Exp(number x) | 訳文 | ネイピア数eのx乗を数値で返します 例:Exp(1)→2.71828182845905, 1/1+Exp(1)^-x→シグモイド関数σ(x) |
| number Log(number x) | 訳文 | xの自然対数を数値で返します 例:Log(Exp(1))→1 |
| number Pow(number b, number p) | 訳文 | bのp乗を数値で返します 例:Pow(5, 2)→25 |
| number Abs(number x) | 訳文 | xの絶対値を数値で返します 例:Abs(-3.14)→3.14 |
| vector Abs(vector v) | 訳文 | vの各要素の絶対値をベクトルで返します 例:Abs(-2, 0.5, -4.44)→(2, 0.5, 4.44) |
| number Sign(number x) | 訳文 | xの符号を数値(-1, 0, 1)で返します 例:Sign(123.123)→1, Sign(-456)→-1, Sign(0)→0 |
| number Round(number x) | 訳文 | xに最も近い整数を数値で返します。小数第一位の四捨五入で最も近い整数が決定します 例:Round(1.499)→1, Round(100.5)→101 |
| number Floor(number x) | 訳文 | xの小数点以下を切り捨てた値を数値で返します 例:Floor(1.499)→1, Floor(100.5)→100 |
| number Ceil(number x) | 訳文 | xの小数点以下を切り上げた値を数値で返します 例:Ceil(1.499)→2, Ceil(100.5)→101 |
| number Max(number a, number b, [number c]) | 訳文 | aとbとcのうち最も大きい数値を返します。cは無くても機能します 例:Max(3.14, 3.1415, 3.141592)→3.141592, Max(3.14, 3.1415)→3.1415 |
| number Min(number a, number b, [number c]) | 訳文 | aとbとcのうち最も小さい数値を返します。cは無くても機能します 例:Max(3.14, 3.1415, 3.141592)→3.14, Min(3.14, 3.1415)→3.14 |
| integer Max(integer a, integer b, [integer c]) | 訳文 | aとbとcのうち最も大きい整数を返します。cは無くても機能します 例:Max(5, 10, 15)→15(int), Max(5, 10)→10(int) |
| integer Min(integer a, integer b, [integer c]) | 訳文 | aとbとcのうち最も小さい整数を返します。cは無くても機能します 例:Min(5, 10, 15)→5(int), Min(5, 10)→5(int) |
| number Max(vector v) | 訳文 | vの成分のうち最大のものを返します 例:Max(a(4, 3, 4))→4 |
| AnyType If(number condition, AnyType if true, AnyType if false) | 訳文 | If構文です。If(数値に関する判定式, 正のとき、偽のとき)のように使います。入れ子にすることで複数の条件分岐が可能です 例:If(a>10,10,a)→aが10を超えたら10のまま、10以下はそのままaを出力する 例:If(a>10,10,if(a<0,0,a))→aが10を超えたら10のまま、10以下のときに0未満であれば0のまま、それ以外はそのままaを出力する |
| AnyType If(integer condition, Anytype if true, Anytype if false) | 訳文 | 上記の関数の整数バージョン |
| text String(AnyType to be a string, [text format code]) | 訳文 | v3.9.0.0で追加 C#のToString()メソッド、簡単に言えばエクセルのデータ形式と同様の働きをします。text format codeは無くても機能します。詳しくはToStringメソッドでの書式指定(Qiita)を見てね(他力本願寺) 例:String(3.14, "c")→"$3.14", String(3.14, "e")→"3.140000e+000", String(3.14, "##.##")→"3.14", String(3.14)→"3.14"(文字列で出力されることに注意!) |
| vector Vector(number x, number y, number z) | 訳文 | x~zを用いて3次元行ベクトルを返します 例:Vector(1, 2, 3)→(1, 2, 3) |
| integer Int(number x) | 訳文 | xを四捨五入して整数xとして返します 例:Int(3.14)→3(int) |
| integer Int(integer x) | 訳文 | xを整数xとして返します。よくわかりませんが安全のため追加されているとのこと 例:Int(3)→3(int) |
| integer Int(text s) | 訳文 | sを整数xとして返します。整数として返せない場合は整数0を返します 例:Int("5")→5(int), Int("3.14")→0(int), Int("abcde")→0(int) |
| number Num(integer x) | 訳文 | xを数値xとして返します 例:Num(4)→4 |
| number Num(number x) | 訳文 | xを数値xとして返します。よくわかりませんが安全のため追加されているとのこと 例:Num(4)→4 |
| number Num(text s) | 訳文 | sを数値xとして返します。数値として返せない場合は数値0を返します 例:Num("3.14")→3.14 |
| vector ToUniversal(vector standard coord) | 訳文 | v3.9.0.0で追加 Positionノードのスタンダード座標(Unityゲームエンジン上の座標)をユニバーサル座標で返します 例(第1入力末端aにPosition[Standard]をつないだ状態で):ToUniversal(a)→(対応した3次元行ベクトル) |
| vector ToStandard(vector universal coord) | 訳文 | v3.9.0.0で追加 Positionノードのユニバーサル座標をスタンダード座標(Unityゲームエンジン上の座標)で返します 例(第1入力末端aにPosition[Universal]をつないだ状態で):ToStandard(a)→(対応した3次元行ベクトル) |
| vector LocalPosToGlobalPos(vector local position, vector parent position, rotation parent rotation) | 訳文 | 自機のローカル座標系での位置をワールド座標系での位置に変換します(※1:編者未使用につき正しくない場合があります) |
| vector GlobalPosToLocalPos(vector global position, vector parent position, rotation parent rotation) | 訳文 | 自機のグローバル座標系での位置をローカル座標系での位置に変換します(※1) |
| rotation LocalRotToGlobalRot(rotation local rotation, rotation parent rotation) | 訳文 | 自機のローカル座標系での回転をグローバル座標系での回転に変換します(※1) |
| rotation GlobalRotToLocalRot(rotation global rotation, rotation parent rotation) | 訳文 | 自機のグローバル座標系での回転をローカル座標系での回転に変換します(※1) |
| vector LocalDirToGlobalDir(vector local direction, rotation parent rotation) | 訳文 | 自機のローカル座標系での方向をグローバル座標系での方向に変換します(※1) |
| vector GlobalDirToLocalDir(vector global direction, rotation parent rotation) | 訳文 | 自機のグローバル座標系での方向をローカル座標系での方向に変換します(※1) |
| rotation FromToRot(vector from, vector to) | 訳文 | 第一引数のベクトルから第二引数のベクトルへの回転をクォータニオンで返します |
| rotation FromEuler(number pitch, number yaw, number roll) | 訳文 | Pitch(x), Roll(y), Yaw(z)の角度をクォータニオンとして返します。x, y, zはOrientation inputから取得しなくても問題ありません |
| rotation FromEuler(vector angles) | 訳文 | ベクトルのx, y, z成分からなるオイラー角をクォータニオンとして返します |
| vector ToEuler(rotation angles) | 訳文 | オイラー角からx, y, zの角度を返します |
| number Angle(rotation r) | 訳文 | クォータニオンからその方向の単位ベクトルの角度を数値として返します(※1) |
| number Angle(vector v, vector w) | 訳文 | ベクトルvとベクトルwの2点間の角度を返します |
| vector Axis(rotation r) | 訳文 | クォータニオンからその方向の単位ベクトルを返します(※1) |
| vector setX(vector vector, number new x) | 訳文 | 第一引数のベクトルのx成分を第二引数で置き換えます(※1) |
| vector setY(vector vector, number new y) | 訳文 | 第一引数のベクトルのy成分を第二引数で置き換えます(※1) |
| vector setZ(vector vector, number new z) | 訳文 | 第一引数のベクトルのz成分を第二引数で置き換えます(※1) |
| vector outputV(number i) | 訳文 | i番目の出力末端における直前のフレームの出力を返します。直前の出力がベクトルでなかった場合は(0, 0, 0)を返します(※1) |
| number output(number i) | 訳文 | i番目の出力末端における直前のフレームの出力を返します。直前の出力が数値でなかった場合は0を返します 例:a,(a>output(1))+output(2)→","で出力先が変わるため、"a"がoutput(1)に格納され、"(a>output(1))+output(2)"がoutput(2)に格納されます。aが0より大きくなると直前のaであるoutput(1)を超えるためa>output(1)がtrueすなわち1となるので1+output(2)の結果がoutput(2)に入ります。これはいわゆるカウンタです(下の方で解説します) |
| Properties 属性(※一部順不同) | ||
| number (vector v).x | 訳文 | ベクトルvのx成分を返します 例(第1入力末端にベクトル(1,2,3)をつないだ状態で):a.x→1 |
| number (vector v).y | 訳文 | ベクトルvのy成分を返します 例(第1入力末端にベクトル(1,2,3)をつないだ状態で):a.y→2 |
| number (vector v).z | 訳文 | ベクトルvのz成分を返します 例(第1入力末端にベクトル(1,2,3)をつないだ状態で):a.z→3 |
| number (rotation q).x | 訳文 | v3.9.0.0で追加 クォータニオンqの第一引数を度数として返します。.xは.pitchと書いても機能します 例(第1入力末端にRotation[Quaternion]をつないだ状態で):a.x→(対応した角度), a.pitch→(a.xと同様の角度) |
| number (rotation q).y | 訳文 | v3.9.0.0で追加 クォータニオンqの第二引数を度数として返します。.yは.yawと書いても機能します 例(第1入力末端にRotation[Quaternion]をつないだ状態で):a.y→(対応した角度) |
| number (rotation q).z | 訳文 | v3.9.0.0で追加 クォータニオンqの第三引数を度数として返します。.zは.rollと書いても機能します 例(第1入力末端にRotation[Quaternion]をつないだ状態で):a.z→(対応した角度) |
| number (vector v).magnitude | 訳文 | ベクトルvの大きさを数値で返します 例(第1入力末端にベクトル(2,4,4)をつないだ状態で):a.magnitude→6 |
| number (vector v).sqrMagnitude | 訳文 | ベクトルvの大きさの2乗を数値で返します 例(第1入力末端にベクトル(2,4,4)をつないだ状態で):a.sqrMagnitude→36 |
| rotation (rotation r).inverse | 訳文 | クォータニオンrの共役クォーニタオンr̅(回転はそのままにxyz軸がすべて反転)を返します 例:(第1入力末端にRotation(0°,356°, 0 ゚ )をつないだ状態で):a.inverse→(0°,4°, 0 ゚ ) |
| Operators 演算子(※一部順不同) | ||
| number (number x) + (number y) | 訳文 | x + y 例:1 + 2→3 |
| integer (integer x) + (integer y) | 訳文 | x + y 例:1(int) + 2(int)→3(int) |
| number (integer x) + (number y) | 訳文 | x + y。整数と数値が逆でも数値が返ってきます 例:1(int) + 2→3, 1 + 2(int)→3 |
| text (text x) + (text y) | 訳文 | v3.8.2.0で追加 x + y 例:"Advanced" + "Cannon"→"AdvancedCannon" |
| vector (vector v) + (vector w) | 訳文 | v + w 例:(1, 2, 3) + (4, 5, 6)→(5, 7, 9) |
| number (number x) - (number y) | 訳文 | x - y 例:1 - 2→-1 |
| integer (integer x) - (integer y) | 訳文 | x - y 例:1(int) - 2(int)→-1(int) |
| number (integer x) - (number y) | 訳文 | x - y。整数と数値が逆でも数値が返ってきます 例:1(int) - 2→-1, 1 - 2(int)→-1 |
| text (text x) - (text y) | 訳文 | x - y。文字列yが1字のときは、文字列xに含まれるすべての文字列yが取り除かれます 例:"AdvancedCannon" - "Cannon"→"Advanced", "aabbabab"-"b"→"aaaa", "aabbabab"-"bb"→"aaabab" |
| vector (vector v) - (vector w) | 訳文 | v - w 例:(1, 2, 3) - (4, 5, 6)→(-3, -3, -3) |
| vector (vector v) x (vector w) | 訳文 | v x w。ベクトル積です 例:Forward(0, 0, 1) - Up(0, 1, 0)→(-1, 0, 0) (※Unityでは左手系のため通常とはベクトルの向きが異なること、Z軸が正面であることに注意しましょう) |
| number (number x) * (number y) | 訳文 | x * y 例:2 * 3→6 |
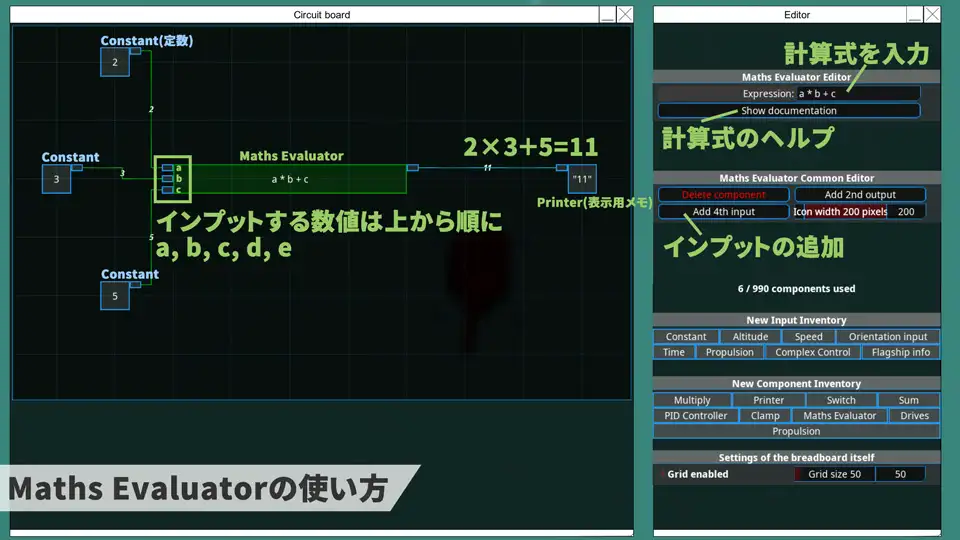
5-1.a,b,c,d,eって何?
インプットの左上から順にa,b,c,d,eの数値に代入されて計算される。
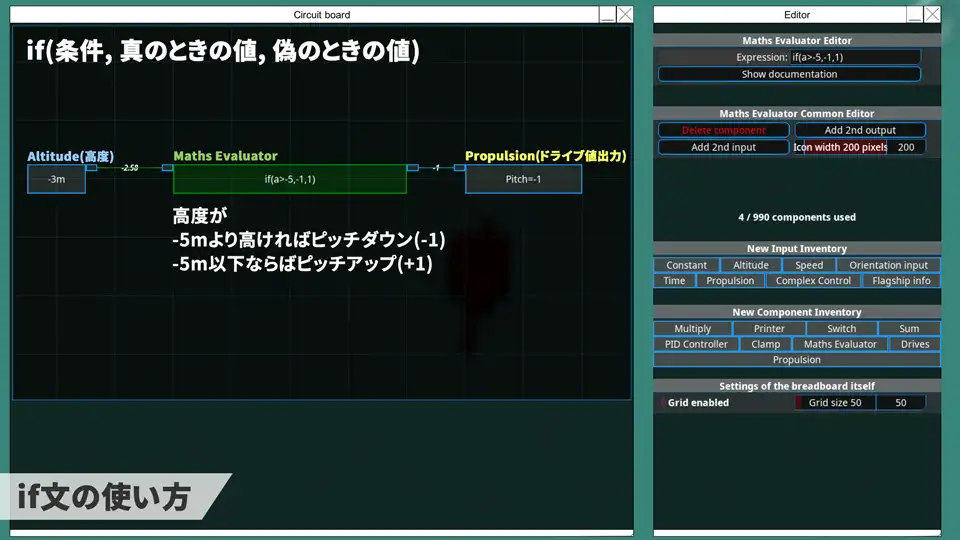
5-2.if文の使い方
if(条件, 真のときの値, 偽のときの値) というふうに使う。Switchよりも使いやすい。
下は水深によってピッチ?を調整してみた例。
5-3.output()の使い方
Bread Board本家ページに詳しく書いてある。
output(1)+1はビークル出現からのフレーム*4数をカウントできて特に便利なので覚えておこう。
5-4. a?b:c構文の使い方
簡単に言うと三項演算子と呼ばれるもので、意味自体はa?b:c=if(a, b, c)と同じ。
プログラムにおいては"if構文"と"三項演算子"で性格が違うため使い勝手が異なるが、FtDのMath Evaluaterにおいては括弧()による可読性の違いで重宝する場合がある。
例えば、if文で入れ子にすると
if(a, b, if(c, d, if(e, f, g)))
のように入れ子×2の数で括弧が増えていって、途中で内側をいじるとどの括弧がどの階層なのか分からないし、実際の式ではa, b, cではなく括弧の絡んだものが入るのでより読みにくいものになる(=可読性の低下)。
一方で、三項演算子では
a ? b : c ? d : e ? f : g
のようになる。結局やってることが複雑なので読みにくいが、if文よりかは読みやすいはず。?と:の間が式なんだと一目で分かるからだ。
5-5. localとparentについて
上記一部関数にはlocal〇〇やparent〇〇といったが引数がある。
6.作成例
6-1.後進ハイドロフォイル
3.2.9にて後進にも対応しました
まず、ブレッドボードを介してハイドロフォイルを操作してみよう。
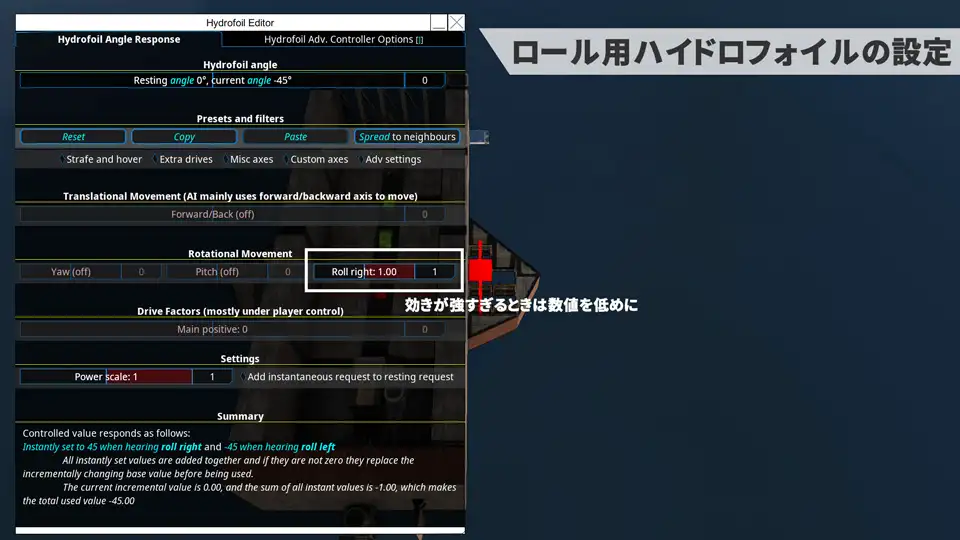
ハイドロフォイルをロール?用に設定し、
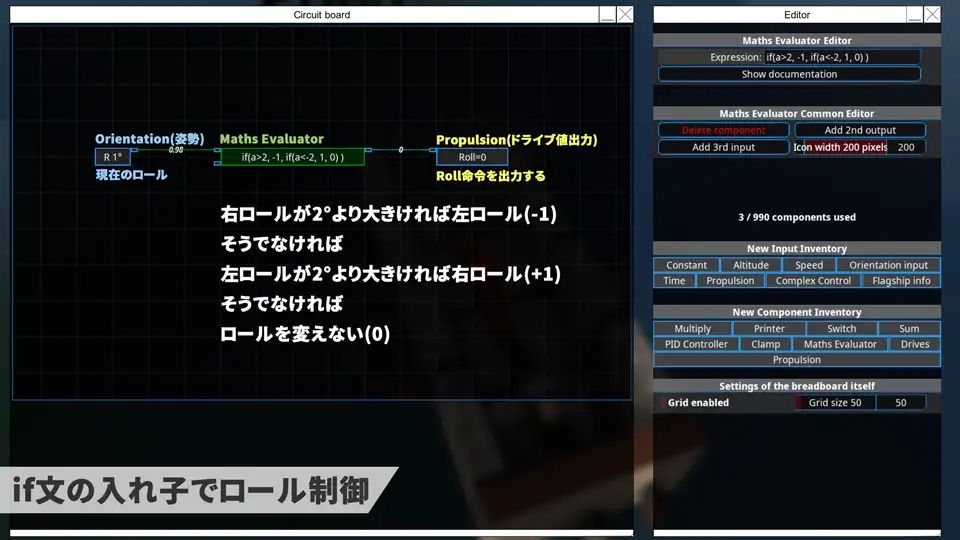
Orientation/Maths Evaluatorコンポーネントを使って条件分岐を書く。
if文を入れ子にして左ロール・右ロール・何もしないの3つの状態を切り替えている。
if(条件1, 条件1のときの値, if(条件2, 条件2のときの値, どちらでもないときの値)) のように書いている。
ここからさらに後進の場合に対応していこう。
ふつうハイドロフォイルはバックの場合に逆向きの力が出てしまい船のバランスを崩してしまう。
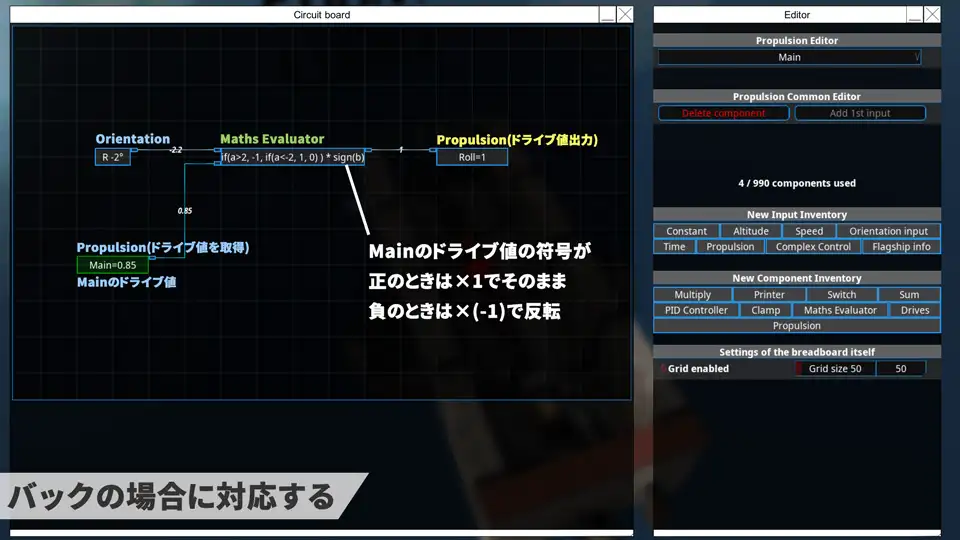
符号を求める関数sign()を使って、
後進の場合はハイドロフォイルを逆に操作するようにかけ算をしてやるとうまくいく。
Propulsion(入力版)とPropulsion(出力版)の見た目が紛らわしいので気を付けて。
6-2.PIDの代わり
AIPIDの代わりはできないが、General Purpose PIDの代わりはできる。
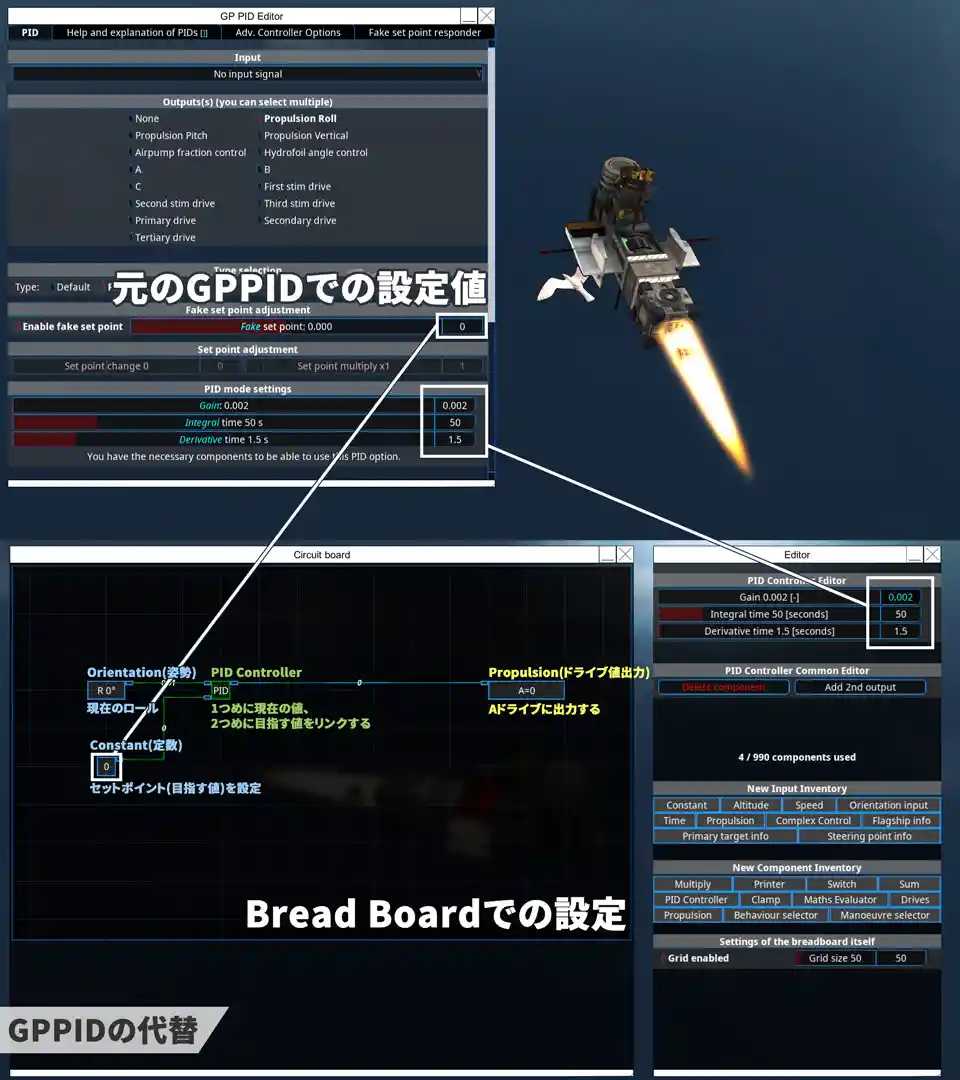
GPPIDでのロール制御をブレッドボードで行うときは、
PID/Orientation/Constantコンポーネントを用いてこのように書くことができる。
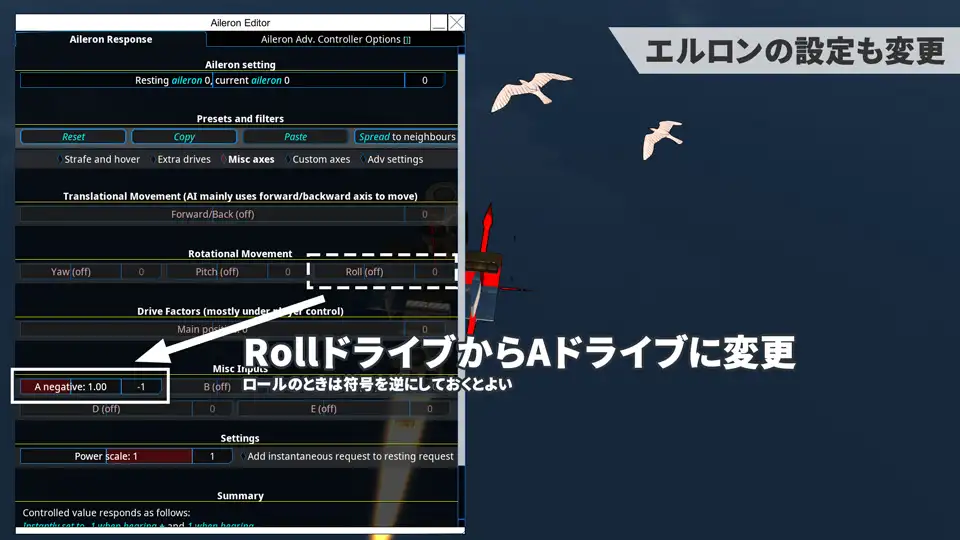
ブレッドボードでは出力値が反転することがあるため、そんなときは設定を左右逆にしておくとよい。
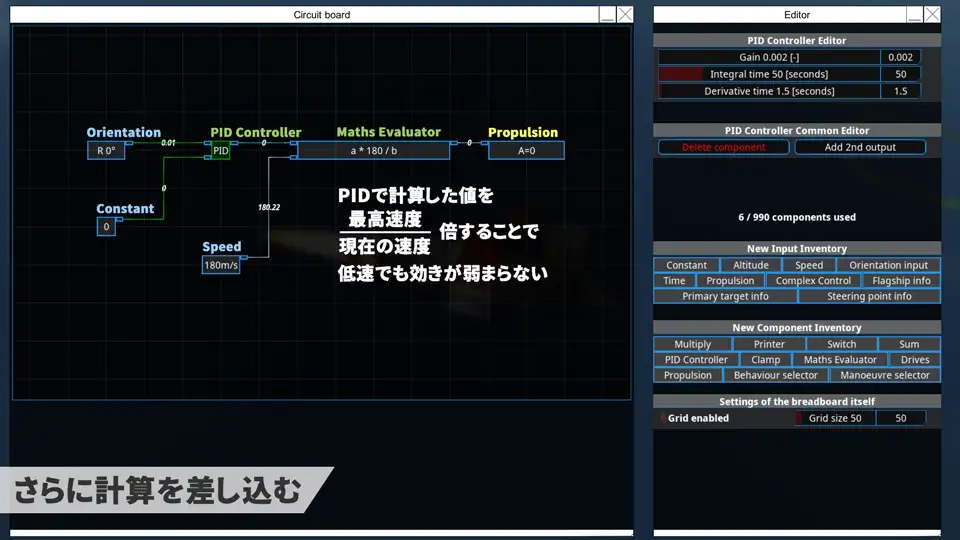
さらに計算を加えていくこともできる。
速度が小さいときに、エルロンの効きを強めるように書いた例。
Constantの目指す値の部分にも計算式を入れればより変幻自在に制御をすることができる。
敵の高度に合わせてこちらの高度を調整したり、色々と試してみよう。
コメント
- 個人的に必要だと思う部分を全力で捕捉しました。分かりやすさのため元ページと書き方がちがう部分がありますのでご注意ください。 -- sosu2357? 2020-12-15 (火) 01:28:36
- 見やすい!わかりやすい!たのしい!ステキ! -- EMR? 2020-12-15 (火) 21:50:47