イベント/晩夏特訓作戦計画

晩夏特訓作戦計画

晩夏特訓作戦計画
期間：2019/08/24 0:00 ~ 2019/09/13 23:59

任務を達成し、パスワードを集めて数字を揃えよう！

概要

• ドールズフロントラインで2回目となるビンゴイベント。
  任務を達成することで「パスワードカード」を入手し、それを使ってビンゴシートのマスを埋めていく。
  ビンゴの各列が埋まる度に資源などの報酬が貰え、
  更に一定数の列を埋めると限定人形や挑戦者勲章などの特別報酬も獲得可能。

過去の類似イベント

ルール

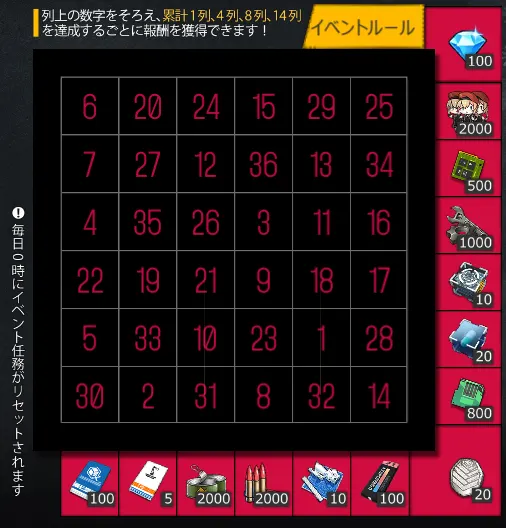
1. パスワードカードを1枚使用することで「乱数解読」を行えます。解読するたびに数字をランダムで1つ獲得できます。
2. 任意のライン上の数字をすべて解読し終えると、そのラインに表示されている報酬を獲得できます。
3. 重複した数字が出た場合は、自動的に10ポイントに変換されます。
4. 100ポイントを使用して「確定解読」を行うと、任意の未解読の数字を1つ獲得できます。
5. 解読済みの数字により一定数のラインに達すると、追加報酬を獲得できます。
6. 日付が変わるとすべてのビンゴ任務はリセットされるので、ご注意ください。
7. イベントが終了すると、パスワードカードとポイントは全て回収されます。
   使わなかったパスワードカードは、カード1枚につき較正チケット5に変換されてメールボックスに贈られます。
   ポイントは一切変換されないため注意。

攻略

• 任務は1日9つ開示される。
• 任務を一つ達成する度に、「パスワード」が入手できる。
  このパスワードを使用することで、ビンゴシートのマスをランダムで1つ開けることが出来る。
• パスワードを使用した際、既に空いている数字が再度出ることもある。
  その場合、「ポイント」を10点入手できる。
  「ポイント」は100点使用することで、任意の数字を1つ開けることが出来る。
• 任務は日替わりであり、達成しなかった任務は翌日には別のものに入れ替わる。
• 序盤、中盤はパスワードを使ってマスを開けつつ点数を貯め、
  終盤、未開示のマスが少なくなってきた時点で点数を使い、ピンポイントでマスを開けていくと良い。
   
• 中国での研究によると、既に開いているマスが出る確率は開いていないマスが出る確率の3倍程度だと予想されている。ソース
  したがって、ポイントは「確定解読を使えば残り全てのマスを開けられる」場面まで我慢して貯めておくのが良いでしょう。

任務一覧

• 任務内容はユーザーによってランダムの模様。情報提供お願いします。
• 基地 > 期間限定イベント > 追加獲得 から確認可能。

参考:任務クリア回数と、埋まるマス数の確率

報酬

ライン達成数	報酬
1ライン報酬	人力x3000 弾薬x3000 配給x3000 パーツx3000
4ライン報酬	人形製造契約x10 快速製造契約x10 快速修復契約x10 快速訓練契約x2
8ライン報酬	★5 SMG「JS 9」
14ライン報酬	挑戦者勲章x1 コインx50 較正チケットx200 上級訓練資料x200

コメント